Sections: Technologie
Buts et objectifs de la leçon :
éducatif: montrer aux élèves comment utiliser la méthode de projection rectangulaire lors de la réalisation d'un dessin ;
• la nécessité d'utiliser trois plans de projection ;
• créer les conditions pour la formation des compétences nécessaires pour projeter un objet sur trois plans de projection ;
développement: développer les concepts spatiaux, la pensée spatiale, l'intérêt cognitif et les capacités créatives des étudiants ;
éduquer : attitude responsable envers le dessin, pour cultiver une culture du travail graphique.
Méthodes et techniques d'enseignement : explication, conversation, situations problèmes, recherche, exercices, travail frontal avec la classe, travail créatif.
Support matériel : ordinateurs, présentation « Projection rectangulaire », tâches, exercices, fiches d'exercices, présentation pour autotest.
Type de cours : cours pour consolider les connaissances.
Travail de vocabulaire : plan horizontal, projection, projection, profil, recherche, projet.
I. Partie organisationnelle.
Énoncez le sujet et le but de la leçon.
Réalisons cours-concours, pour chaque tâche vous recevrez un certain nombre de points. En fonction des points marqués, une note pour la leçon sera attribuée.
II. Répétition de la projection et ses types.
La projection est le processus mental de construction d’images d’objets sur un plan.
La répétition s'effectue à l'aide de la présentation.
1. Il est demandé aux étudiants situation problématique. (Présentation 1)
Analysez la forme géométrique de la pièce sur la projection frontale et retrouvez cette pièce parmi les images visuelles.

De cette situation, on conclut que les 6 parties ont la même projection frontale. Cela signifie qu'une seule projection ne donne pas toujours une image complète de la forme et du design de la pièce.
- Quelle est la sortie de cette situation ? (Regardez la partie de l'autre côté).
2. Il était nécessaire d'utiliser un autre plan de projection. (Projection horizontale).
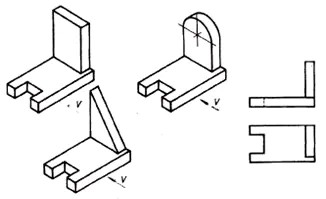
3. Le besoin d'une troisième projection se fait sentir lorsque deux projections ne suffisent pas pour déterminer la forme d'un objet.
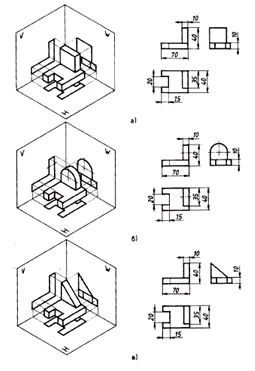
Dimensionnement :
- sur la projection frontale –
Conclusion : cela signifie que pour apprendre à faire des dessins, il faut être capable de projeter des objets sur un plan.
Remplissez les mots manquants dans le texte de définition.
1. Il existe des projections _______________ et ______________.
2. Si ______________ rayons sortent d’un point, la projection est appelée ______________.
3. Si ______________ rayons sont dirigés parallèlement, la projection est appelée _____________.
4. Si les rayons ______________ sont dirigés parallèlement les uns aux autres et à un angle de 90 ° par rapport au plan de projection, alors la projection est appelée ______________.
5. Une image naturelle d'un objet sur un plan de projection n'est obtenue qu'avec la projection ______________.
6. Les projections sont situées les unes par rapport aux autres____________________________________________.
7. Le fondateur de la méthode de projection rectangulaire est _______________
Tâche 2. Projet de recherche
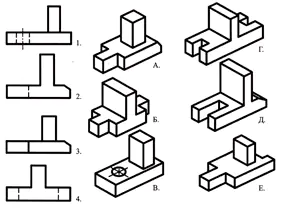
Associez les principaux types indiqués par des chiffres avec les parties indiquées par des lettres et écrivez la réponse dans votre cahier.
Un exercice pour réviser la connaissance des corps géométriques.
À l’aide de la description verbale, trouvez une image visuelle de la pièce.
La base de la pièce a la forme d'un parallélépipède rectangle dont les plus petites faces présentent des rainures en forme de prisme quadrangulaire régulier. Au centre de la face supérieure du parallélépipède se trouve un cône tronqué, le long de l'axe duquel se trouve un trou cylindrique traversant.
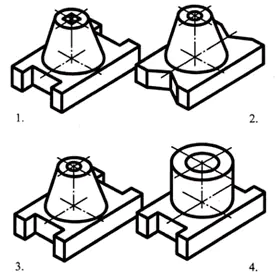
Réponse : partie n°3 (1 point)
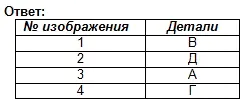
Trouver la correspondance entre les dessins techniques des pièces et leurs projections frontales (le sens de projection est marqué par une flèche). Sur la base des images dispersées du dessin, réalisez un dessin de chaque partie, composé de trois images. Écrivez votre réponse dans le tableau (Fig. 129).
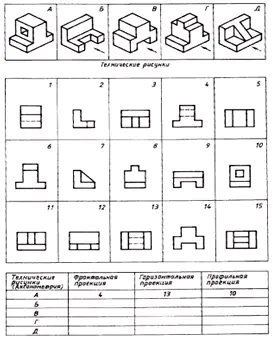
| Dessins technique | Projection frontale | Projection horizontale | Projection de profil |
| UN | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| DANS | 14 | 5 | 1 |
| g | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Travaux pratiques.
Tâche n°1. Projet de recherche
Trouvez les projections frontales et horizontales de cette image visuelle. Écrivez la réponse dans votre cahier.
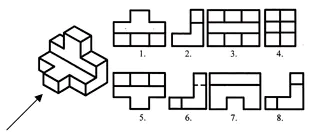
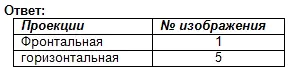
Évaluation du travail dans la leçon. Auto-test. (Présentation 2)
Les points de notation de la première partie du travail sont inscrits au tableau :
Tâche n°2. Travail de création et vérification de sa mise en œuvre
(projet créatif)
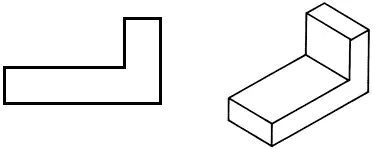
• Dessinez la projection frontale dans votre cahier d'exercices.
• Dessinez une projection horizontale, en changeant la forme de la pièce afin de réduire sa masse.
• Si nécessaire, apportez des modifications à la projection frontale.
• Pour vérifier que la tâche est terminée, appelez un ou deux élèves au tableau pour expliquer leur solution au problème.
IV. Résumer la leçon.
1. Évaluation du travail dans la leçon. (Vérification de la partie pratique du travail)
V. Devoirs à la maison.
1. Projet de recherche.
Travaillez selon le tableau : déterminez quel dessin, désigné par un chiffre, correspond au dessin, désigné par une lettre.
Un cas particulier de projection parallèle, dans lequel la direction de projection est perpendiculaire au plan de projection, est appelé rectangulaire ou projection orthogonale. La projection rectangulaire (orthogonale) d'un point est la base de la perpendiculaire tracée du point au plan de projection. La projection rectangulaire des points A et B est représentée sur la Fig. 5.
Pour déterminer la position d'un point dans l'espace à partir de ses projections parallèles, il faut disposer de deux plans parallèles obtenus dans deux directions de projection.
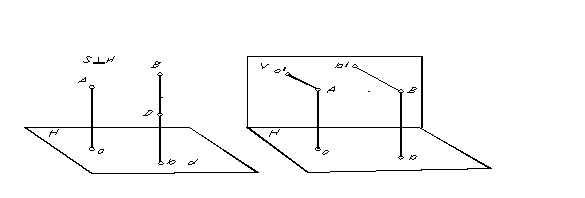 |
Parce que passant par un point, une seule droite perpendiculaire au plan peut être tracée, alors, évidemment, avec projection orthogonale, pour obtenir deux projections d'un point, il faut avoir deux plans de projection non parallèles (Fig. 6) .
La projection orthographique présente de nombreux avantages par rapport à la projection centrale et parallèle. Il s'agit principalement de :
1. Simplicité des constructions graphiques pour déterminer des projections orthogonales de points.
2. La capacité, sous certaines conditions, de conserver la forme et la taille de la figure projetée sur les projections.
Les avantages constatés ont assuré l'utilisation généralisée de la projection orthogonale dans la technologie, en particulier pour la préparation de dessins d'ingénierie mécanique.
En génie mécanique, afin de pouvoir juger à partir d'un dessin de la forme et de la taille des objets représentés, lors de l'élaboration de dessins, ils utilisent généralement non pas deux, mais plusieurs plans de projection.
La position d'un point dans l'espace, et donc de toute figure géométrique, peut être déterminée si un système de référence de coordonnées est spécifié. Les plans de projection divisent l'espace en huit parties - les octants. Ils sont classiquement numérotés en chiffres romains (Fig. 7).
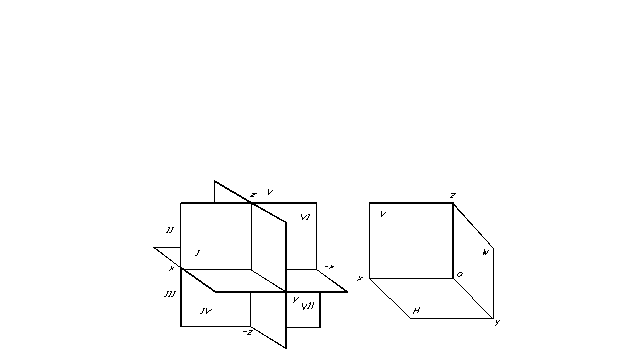
Les plans de projection divisent l'espace en huit parties - les octants. Ils sont classiquement numérotés en chiffres romains (Fig. 7).
Le plus pratique pour fixer la position d'une figure géométrique dans l'espace et identifier sa forme à partir de projections orthogonales est le système de coordonnées cartésiennes, composé de trois plans de projection mutuellement perpendiculaires. Étant donné que la géométrie descriptive est conçue pour transmettre les résultats de ses recherches théoriques à une utilisation pratique, il est conseillé d'envisager également la projection orthogonale dans un système de trois plans de projection.
Pour faciliter la projection, trois plans mutuellement perpendiculaires sont choisis comme trois plans de projection (Fig. 8). L'un d'eux est généralement placé horizontalement - on l'appelle plan de projection horizontal, l'autre est vertical, parallèle au plan de dessin, on l'appelle plan frontal des projections et un troisième, perpendiculaire aux deux existants - on l'appelle plan de profil des projections. Ces plans de projection se coupent le long de lignes appelées axes de projection.
Nous avons adopté un système droitier pour disposer les plans de projection. Dans ce cas, on considère les directions positives des axes : pour l'axe X (intersection des plans de projection horizontal et frontal) – à gauche de l'origine, pour l'axe oui (intersection des plans de projection horizontal et de profil) – vers l'observateur depuis le plan de projection frontal, pour l'axe z (intersection des plans frontaux et profilés des projections) – vers le haut à partir du plan horizontal des projections, les directions opposées des axes sont considérées comme négatives.
La projection d'un point est la base de la perpendiculaire tracée du point sur le plan de projection correspondant. Projection horizontale les points sont la projection rectangulaire d'un point sur un plan de projection horizontal, projection frontale – respectivement sur le plan frontal des projections et profil - sur le plan de profil des projections.
Il n'est pas pratique d'utiliser cette disposition spatiale pour représenter des projections orthogonales de figures géométriques en raison de son encombrement, mais également du fait que sur les projections individuelles (horizontales et de profil), la forme et la taille de la figure projetée sont déformées. Par conséquent, au lieu de représenter une disposition spatiale dans un dessin, ils utilisent un dessin complexe (diagramme de Monge) composé de trois projections orthogonales interconnectées d’une figure géométrique.
La transformation de l'agencement spatial en schémas s'effectue en combinant les plans de projection horizontal et de profil avec le plan de projection frontal (Fig. 7).
Les plans n'ayant pas de frontières, dans la position combinée (sur le schéma) les limites des plans ne sont pas représentées, il n'est pas nécessaire de laisser des inscriptions indiquant la position des plans de projection (Fig. 10).
En passant au diagramme, la clarté spatiale a été perdue. Le diagramme donne plus : précision et facilité de mesure des images, avec simplicité de construction. Cependant, imaginer une image spatiale nécessite un travail d’imagination.
Vous n'avez pas trouvé ce que vous cherchiez ? Utilisez la recherche :
Meilleurs dictons : Pour un étudiant, le plus important n'est pas de réussir l'examen, mais de s'en souvenir à temps. 9744 — | 7364 - ou lisez tout.
Dessin par projection (bases de la géométrie descriptive)
Méthode de projection
Méthode de projection rectangulaire
Si les rayons projetés forment un angle droit avec le plan de projection, alors ces projections sont appelées rectangulaire.
Les projections rectangulaires sont également appelées orthogonal. Le mot « orthogonal » vient des mots grecs « ortos » – droit et « gonia » – angle.
Les dessins dans le système de projections rectangulaires donnent une image complète de la forme et de la taille de l'objet. Elles sont plus faciles à réaliser que les projections axonométriques.
Que faut-il savoir pour réussir ses dessins ?
Tout objet ayant des surfaces planes est limité par des sommets, des arêtes et des faces (Fig. 108). Par conséquent, pour apprendre à représenter divers objets dans des dessins, vous devez savoir comment les sommets (points), les arêtes (segments de lignes droites) et les arêtes d'objets (parties d'un plan) sont représentés dans des projections rectangulaires.
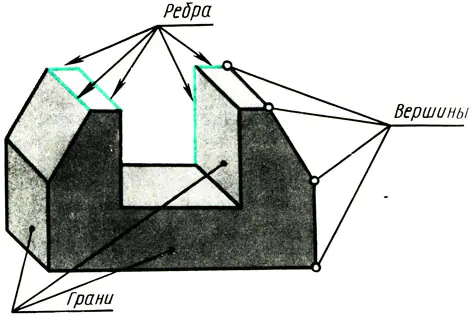
Riz. 108. Premsch comme un ensemble de points, écrivez. Sommets des avions
Faisons une expérience simple. Voyons comment un objet plat et une centaine d'éléments sont représentés dans différentes positions.
Prenons le mur opposé à la fenêtre comme plan de projection. Laisse-le par la fenêtre perpendiculaire Des rayons de lumière tombent sur le mur – projetant des rayons. Placez une feuille de papier ABCD épais devant le mur (parallèle à celui-ci) (Fig. 109, a). Une ombre se forme sur le mur, équivalente à la projection de l'objet. Quelles sont ses dimensions ? Dans ce cas, la projection a’b’c’d’ correspond en forme et en taille à l’objet de projection – la feuille
A B C D. La méthode de projection est rectangulaire, puisque les rayons projetés sont perpendiculaires au plan de projection.
Comment la projection changera-t-elle si l'objet représenté tourne, par exemple, autour de sa hauteur - bord AD (Fig. 109, b) ?
En tournant, l’ombre diminuera en largeur (les lignes a’b’ et c’d’ sur la Fig. 109, b deviennent plus courtes). En continuant à faire pivoter la feuille de papier, on constate qu'en position perpendiculaire au mur, l'image de la feuille se transformera en une ligne (Fig. 109, c), mais la hauteur de l'objet reste constante, c'est-à-dire lignes a' d' et b'c' sur la longueur ne sont pas déformés.
Formulons maintenant des conclusions sur la forme et la taille des images d'un objet plat dans des projections rectangulaires, situées différemment par rapport au plan de projection :
a) une figure plate parallèle au plan de projection y est représentée en grandeur nature (Fig. 109, a) ;
b) une figure plate, inclinée par rapport au plan de projection, y est représentée avec une distorsion des dimensions (Fig. 109, b) ;
c) une figure plate perpendiculaire au plan de projection y est représentée sous la forme d'un segment de droite (Fig. 109, c).
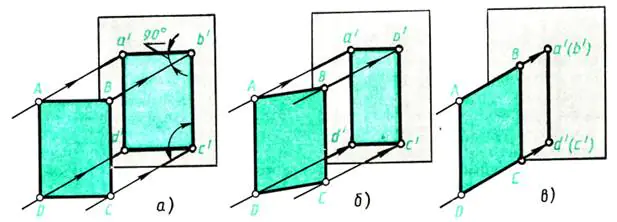
Riz. 109. Projeter une silhouette plate
Ces découvertes concernent la représentation des bords des objets.
Comment les bords des objets, c'est-à-dire les lignes, sont-ils représentés dans des projections rectangulaires ?
Répétons l'expérience de rotation d'un objet plat, observons comment ses bords, c'est-à-dire ses lignes, sont projetés et tirons des conclusions :
a) un segment de droite parallèle au plan de projection y est représenté en taille naturelle (comparez la hauteur de l'objet AD et BC sur la Fig. 109, a, b, c avec ses projections a'd' et b'c, et la largeur de l'objet AB et CD avec ses projections a'b' et c'd' sur la Fig. 109, a) ;
b) un segment droit incliné par rapport au plan de projection y est représenté avec une distorsion en longueur (comparez la largeur de l'objet AB et CD sur la Fig. 109, b avec ses projections a'b' et c'd') ;
c) un segment de droite perpendiculaire au plan de projection est représenté par un point dessus (voir sur la Fig. 109, sur toute la largeur de l'objet - lignes AB et CD, perpendiculaires au plan de projection).
La projection d'un point est la base d'une perpendiculaire abaissée d'un point donné de l'espace sur le plan de projection (voir points a', b', c', d' - projections des points A, B, C, D).
Acceptons de désigner les points dans l'espace par les lettres majuscules A, B, C, D, etc., et les projections de points par les lettres minuscules correspondantes i, b, c, d, etc.
Parmi les deux points coïncidant dans le dessin (Fig. 109, c), l'un est l'image d'un sommet visible et l'autre est invisible (fermé). La désignation des projections de sommets invisibles est prise entre parenthèses.



