Sekce: Technika
Cíle a cíle lekce:
vzdělávací: ukázat žákům, jak používat metodu pravoúhlého promítání při tvorbě výkresu;
• nutnost použití tří promítacích rovin;
• vytvářet podmínky pro utváření dovedností promítat předmět na tři promítací roviny;
rozvíjející se: rozvíjet prostorové představy, prostorové myšlení, kognitivní zájem a tvůrčí schopnosti žáků;
vzdělávat: zodpovědný přístup ke kresbě, pěstovat kulturu grafické práce.
Metody a techniky výuky: vysvětlování, rozhovor, problémové situace, výzkum, cvičení, frontální práce s třídou, kreativní práce.
Materiální podpora: počítače, prezentace „Obdélníkové promítání“, úkoly, cvičení, cvičební karty, prezentace k autotestu.
Typ lekce: lekce k upevnění znalostí.
Práce se slovní zásobou: horizontální rovina, projekce, projekce, profil, výzkum, projekt.
I. Organizační část.
Uveďte téma a účel lekce.
Pojďme provést lekce-soutěž, za každý úkol získáte určitý počet bodů. V závislosti na dosažených bodech bude přidělena známka za lekci.
II. Přehled projekce a jejích typů.
Projekce je mentální proces vytváření obrazů objektů v rovině.
Opakování se provádí pomocí prezentace.
1. Žádají se studenti problematická situace. (Prezentace 1)
Analyzujte geometrický tvar součásti na přední projekci a najděte tuto součást mezi vizuálními obrázky.

Z této situace se usuzuje, že všech 6 dílů má stejnou čelní projekci. To znamená, že jedna projekce ne vždy poskytuje úplný obraz o tvaru a designu součásti.
- Jaké je východisko z této situace? (Podívejte se na část z druhé strany).
2. Bylo potřeba použít jinou projekční rovinu. (Horizontální projekce).
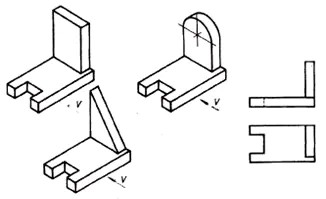
3. Potřeba třetí projekce vzniká, když dvě projekce nestačí k určení tvaru předmětu.
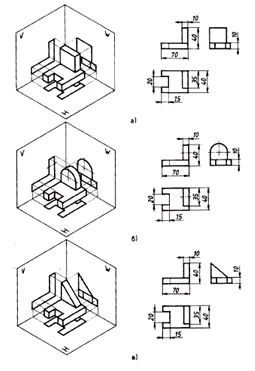
Velikost:
- na čelní projekci –
Závěr: to znamená, že abyste se naučili kreslit, musíte být schopni promítat objekty do roviny.
Doplňte chybějící slova v textu definice.
1. Existuje _______________ a _______________ projekce.
2. Pokud z jednoho bodu vychází _______________ paprsků, projekce se nazývá ______________.
3. Pokud _______________ paprsky směřují rovnoběžně, promítání se nazývá ______________.
4. Pokud _______________ paprsky směřují vzájemně rovnoběžně a pod úhlem 90° k promítací rovině, pak se promítání nazývá ______________.
5. Přirozený obraz předmětu na promítací rovině se získá pouze při ______________ projekci.
6. Výstupky jsou umístěny vůči sobě_______________________________.
7. Zakladatelem metody pravoúhlého promítání je ________________
Úkol 2. Výzkumný projekt
Spojte hlavní typy označené čísly s částmi označenými písmeny a napište odpověď do sešitu.
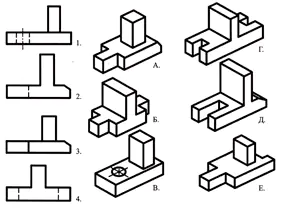
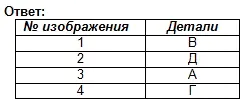
Cvičení k opakování znalostí o geometrických tělesech.
Pomocí slovního popisu najděte vizuální obrázek součásti.
Základna dílu má tvar pravoúhlého rovnoběžnostěnu, jehož menší čela mají drážky ve tvaru pravidelného čtyřbokého hranolu. Uprostřed horního čela kvádru je komolý kužel, podél jehož osy je průchozí válcový otvor.
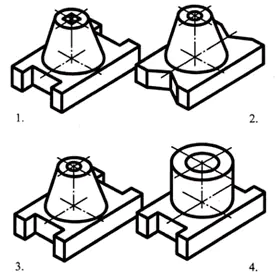
Odpověď: část č. 3 (1 bod)
Najděte shodu mezi technickými výkresy dílů a jejich čelními průměty (směr průmětu je označen šipkou). Na základě rozptýlených obrázků výkresu vytvořte výkres každého dílu, který se skládá ze tří obrázků. Svou odpověď zapište do tabulky (obr. 129).
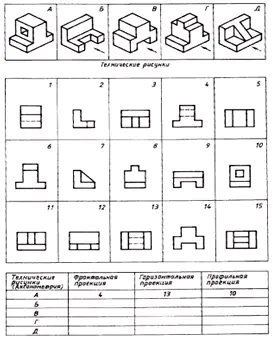
| Technické výkresy | Čelní projekce | Horizontální projekce | Projekce profilu |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| V | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktická práce.
Úkol č. 1. Výzkumný projekt
Najděte čelní a horizontální projekci tohoto vizuálního obrazu. Odpověď napište do sešitu.
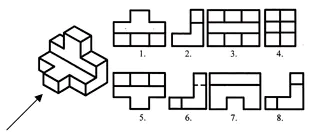
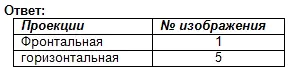
Hodnocení práce v hodině. Autotest. (Prezentace 2)
Body pro hodnocení první části práce se zapisují na tabuli:
Úkol č. 2. Tvůrčí práce a ověřování její realizace
(kreativní projekt)
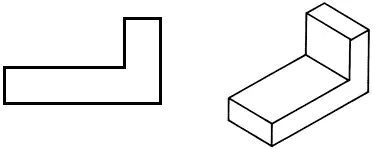
• Nakreslete čelní projekci do sešitu.
• Nakreslete vodorovnou projekci a změňte tvar součásti za účelem snížení její hmotnosti.
• V případě potřeby proveďte změny přední projekce.
• Chcete-li zkontrolovat dokončení úkolu, zavolejte jednoho nebo dva studenty k tabuli, aby vysvětlili své řešení problému.
IV. Shrnutí lekce.
1. Hodnocení práce v hodině. (Kontrola praktické části práce)
V. Zadání domácího úkolu.
1. Výzkumný projekt.
Pracujte podle tabulky: určete, který výkres označený číslem odpovídá výkresu označenému písmenem.
Zvláštní případ rovnoběžného promítání, kdy směr promítání je kolmý na promítací rovinu, se nazývá obdélníkový nebo ortogonální projekce. Pravoúhlý (pravoúhlý) průmět bodu je základna kolmice vedené z bodu do promítací roviny. Pravoúhlý průmět bodů A a B je na Obr. 5.
Pro určení polohy bodu v prostoru z jeho rovnoběžných průmětů je nutné mít dvě rovnoběžné roviny získané ve dvou směrech průmětu.
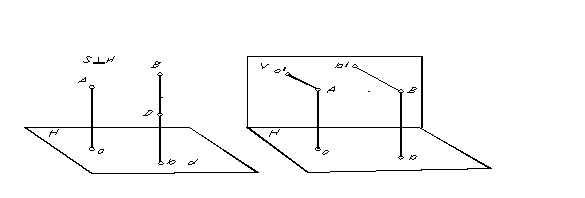 |
Protože bodem lze nakreslit pouze jednu přímku kolmou k rovině, pak samozřejmě při pravoúhlém promítání, abychom získali dva průměty jednoho bodu, je nutné mít dvě nerovnoběžné promítací roviny (obr. 6) .
Ortografické promítání má oproti středovému a paralelnímu promítání řadu výhod. Patří mezi ně především:
1. Jednoduchost grafických konstrukcí pro určování pravoúhlých průmětů bodů.
2. Schopnost za určitých podmínek zachovat tvar a velikost promítaného obrazce na projekcích.
Uvedené výhody zajistily široké použití ortogonálního promítání v technologii, zejména pro přípravu strojírenských výkresů.
Ve strojírenství, aby bylo možné z výkresu posoudit tvar a velikost zobrazených předmětů, při kreslení výkresů zpravidla nepoužívají dvě, ale několik promítacích rovin.
Polohu bodu v prostoru, a tedy jakéhokoli geometrického útvaru, lze určit, pokud je zadán jakýkoli souřadnicový referenční systém. Projekční roviny rozdělují prostor na osm částí - oktantů. Jsou konvenčně číslovány římskými číslicemi (obr. 7).
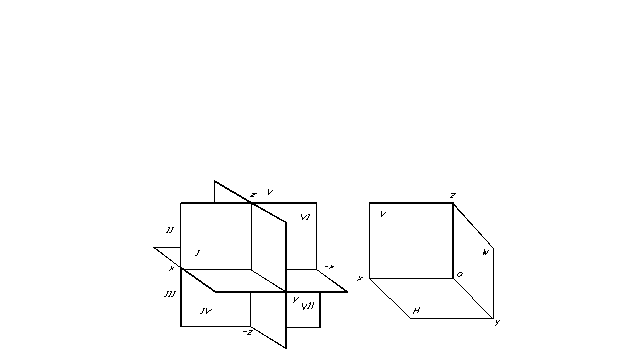
Projekční roviny rozdělují prostor na osm částí - oktantů. Jsou konvenčně číslovány římskými číslicemi (obr. 7).
Nejvhodnější pro fixaci polohy geometrického útvaru v prostoru a identifikaci jeho tvaru z pravoúhlých průmětů je kartézský souřadnicový systém sestávající ze tří vzájemně kolmých promítacích rovin. Vzhledem k tomu, že deskriptivní geometrie je navržena tak, aby zprostředkovala výsledky svého teoretického výzkumu praktickému využití, je vhodné uvažovat s ortogonálním promítáním i v soustavě tří promítacích rovin.
Pro usnadnění promítání jsou jako tři promítací roviny zvoleny tři vzájemně kolmé roviny (obr. 8). Jeden z nich je obvykle umístěn vodorovně - je to tzv horizontální projekční rovina, druhá je svislá, rovnoběžná s rovinou výkresu, nazývá se frontální rovina projekcí a třetí, kolmá ke dvěma stávajícím – je tzv profilová rovina projekcí. Tyto promítací roviny se protínají podél linií tzv projekční osy.
Přijali jsme pravotočivý systém pro uspořádání promítacích rovin. V tomto případě jsou uvažovány kladné směry os: pro osu X (průsečík horizontální a čelní promítací roviny) – vlevo od počátku, pro osu y (průsečík horizontální a profilové promítací roviny) – směrem k pozorovateli z čelní promítací roviny, pro os. z (průsečík čelní a profilové roviny průmětů) – směrem nahoru od vodorovné roviny průmětů jsou opačné směry os považovány za záporné.
Průmět bodu je základna kolmice vedené z bodu do odpovídající promítací roviny. Horizontální projekce body jsou pravoúhlý průmět bodu na vodorovnou projekční rovinu, čelní projekce – respektive na čelní rovině průmětů a profil – na profilovou rovinu projekcí.
Využití tohoto prostorového uspořádání pro zobrazení ortogonálních průmětů geometrických obrazců je nepohodlné pro jeho objemnost a také proto, že na jednotlivých (horizontálních i profilových) dochází ke zkreslení tvaru a velikosti promítaného obrazce. Místo zobrazení prostorového uspořádání ve výkresu proto používají komplexní výkres (Mongeův diagram) složený ze tří vzájemně propojených ortogonálních průmětů geometrického obrazce.
Transformace prostorového uspořádání do schémat se provádí kombinací vodorovné a profilové promítací roviny s čelní promítací rovinou (obr. 7).
Protože roviny nemají žádné hranice, v kombinované poloze (na schématu) nejsou hranice rovin znázorněny, není třeba zanechávat nápisy označující polohu promítacích rovin (obr. 10).
Po přepnutí na diagram se ztratila prostorová jasnost. Diagram poskytuje více - přesnost a snadnost měření snímků s jednoduchostí konstrukce. Představit si prostorový obraz však vyžaduje práci představivosti.
Nenašli jste, co jste hledali? Použijte vyhledávání:
Nejlepší výroky: Pro studenta není nejdůležitější zkoušku složit, ale včas si na ni vzpomenout. 9744 — | 7364 - nebo si přečtěte vše.
Projekční kresba (základy deskriptivní geometrie)
Projekční metoda
Metoda pravoúhlého promítání
Pokud promítající paprsky svírají s promítací rovinou pravý úhel, pak se takové průměty nazývají obdélníkový.
Také se nazývají pravoúhlé projekce ortogonální. Slovo "ortogonální" pochází z řeckých slov "ortos" - rovný a "gonia" - úhel.
Kresby v systému pravoúhlých průmětů dávají ucelený obraz o tvaru a velikosti předmětu. Jsou snadněji proveditelné než axonometrické projekce.
Co potřebujete vědět pro úspěšné dokončení výkresů?
Každý objekt, který má rovné povrchy, je omezen vrcholy, hranami a plochami (obr. 108). Proto, abyste se naučili zobrazovat různé objekty na výkresech, musíte vědět, jak jsou vrcholy (body), hrany (úseky přímek) a hrany objektů (části roviny) zobrazeny v pravoúhlých projekcích.
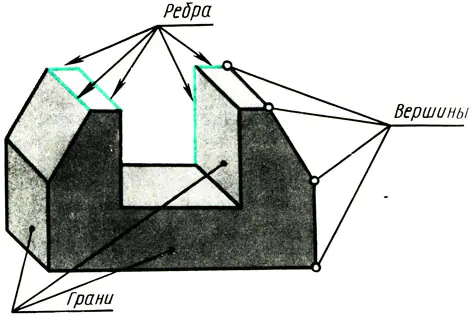
Rýže. 108. Premsch jako soubor bodů, napište. Vrcholy rovin
Udělejme jednoduchý experiment. Podívejme se, jak je plochý předmět a sto prvků zobrazeno v různých pozicích.
Vezměme zeď naproti oknu jako projekční rovinu. Pusť to z okna kolmý Paprsky světla dopadají na stěnu - promítající paprsky. Před stěnu (rovnoběžně s ní) položte list silného papíru ABCD (obr. 109, a). Na stěně se vytvoří stín, ekvivalentní projekci předmětu. Jaké má rozměry? V tomto případě projekce a’b’c’d’ odpovídá tvarem a velikostí předmětu projekce – listu
ABECEDA. Metoda promítání je pravoúhlá, protože promítané paprsky jsou kolmé k promítací rovině.
Jak se změní projekce, když se zobrazený objekt otočí např. kolem jeho výšky - hrany AD (obr. 109, b)?
Při otáčení se stín zmenší do šířky (čáry a’b’ a c’d’ na obr. 109, b se zkrátí). Při dalším otáčení listu papíru si všimneme, že v poloze kolmé ke stěně se obraz listu změní na čáru (obr. 109, c), ale výška předmětu zůstává konstantní, tj. čáry a' d' a b'c' podél délky nejsou zkreslené.
Nyní zformulujme závěry o tom, jaký tvar a velikost má plochý objekt v pravoúhlých projekcích, které jsou různě umístěny ve vztahu k projekční rovině:
a) plochý obrazec rovnoběžný s promítací rovinou je na něm vyobrazen v přirozené velikosti (obr. 109, a);
b) je na něm znázorněna plochá postava nakloněná k promítací rovině se zkreslením rozměrů (obr. 109, b);
c) je na něm znázorněn plochý obrazec kolmý k promítací rovině ve formě úsečky (obr. 109, c).
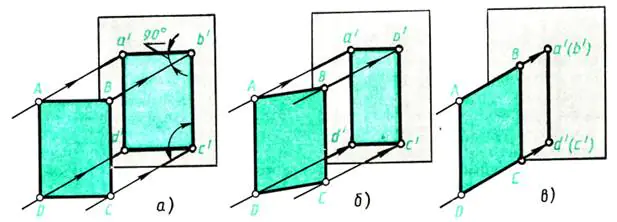
Rýže. 109. Promítání ploché postavy
Tyto poznatky se týkají zobrazení okrajů předmětů.
Jak se v pravoúhlých průmětech zobrazují okraje objektů, tedy čáry?
Zopakujme pokus s otáčením plochého předmětu, pozorujme, jak se promítají jeho hrany, tedy čáry, a vyvodíme závěry:
a) je na něm znázorněna přímka rovnoběžná s promítací rovinou v přirozené velikosti (srovnejte výšku objektu AD a BC na obr. 109, a, b, c s jeho průměty a'd' a b'c, a šířku objektu AB a CD s jeho průměty a'b' a c'd' na obr. 109, a);
b) je na něm znázorněn přímý úsek nakloněný k promítací rovině s délkovým zkreslením (srovnejte šířku předmětu AB a CD na obr. 109, b s jeho průměty a’b’ a c’d’);
c) úsečka kolmá k promítací rovině je na ní znázorněna bodem (viz obr. 109 přes šířku předmětu - úsečky AB a CD, kolmé k promítací rovině).
Průmět bodu je základna kolmice spuštěné z daného bodu v prostoru do průmětny (viz body a’, b’, c’, d’ - průměty bodů A, B, C, D).
Dohodněme se, že body v prostoru budeme označovat velkými písmeny A, B, C, D atd. a průměty bodů odpovídajícími malými písmeny i, b, c, d atd.
Ze dvou bodů, které se shodují na obrázku (obr. 109, c), je jeden obrazem viditelného vrcholu a druhý je neviditelný (uzavřený). Označení průmětů neviditelných vrcholů je převzato v závorce.



