Розділи: Технологія
Цілі та завдання уроку:
навчальна: показати учням використання методу прямокутного проектування під час виконання креслення;
• необхідність застосування трьох площин проекцій;
• створити умови на формування умінь проектувати предмет втричі площини проекцій;
розвиваюча: розвивати просторові уявлення, просторове мислення, пізнавальний інтерес та творчі здібності учнів;
яка виховує: відповідальне ставлення до креслення, виховувати культуру графічної праці.
Методи, прийоми навчання: пояснення, бесіда, проблемні ситуації, дослідження, вправи, фронтальна робота із класом, творча робота.
Матеріальне забезпечення: комп'ютери, презентація "Прямокутне проектування", завдання, вправи, картки з вправою, презентація для самоперевірки.
Тип уроку: урок закріплення знань.
Словникова робота: горизонтальна площина, проекція, проектування, профільна, дослідницький, проект.
I. Організаційна частина.
Повідомлення теми та мети уроку.
Проведемо урок-змагання, за кожне завдання ви отримуватимете певну кількість балів. Залежно від набраних балів буде виставлено оцінку за урок.
ІІ. Повторення про проектування та його види.
Проеціювання - це розумовий процес побудови зображень предметів на площині.
Повторення здійснюється за допомогою презентації.
1. Перед учнями ставиться проблемна ситуація. (Презентація 1)
Проаналізуйте геометричну форму деталі на фронтальній проекції та знайдіть цю деталь серед наочних зображень.

З ситуації робиться висновок, що це 6 деталей мають однакову фронтальну проекцію. Значить, одна проекція не завжди дає повне уявлення про форму та конструкцію деталі.
— Який вихід із цієї ситуації? (Подивитися на деталь з іншого боку).
2. Виникла потреба застосування ще однієї площини проекцій. (Горизонтальна проекція).
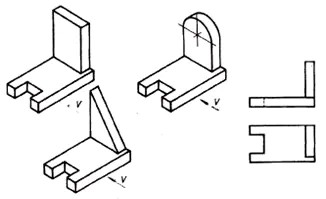
3. Необхідність у третій проекції виникає тоді, як і двох проекцій буває недостатньо визначення форми предмета.
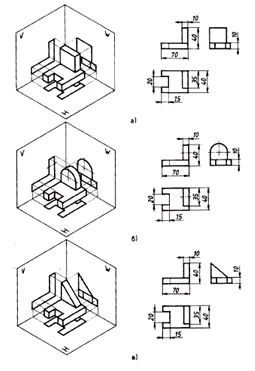
Постановка розмірів:
- на фронтальній проекції –
Висновок: отже, щоб навчитися виконувати креслення, потрібно вміти проектувати предмети на площину.
Вставте пропущені слова у текст визначень.
1. Існує _______________ та ______________ проектування.
2. Якщо ______________ промені виходять із однієї точки, проектування називається ______________.
3. Якщо ______________ промені спрямовані паралельно, проектування називається _____________.
4. Якщо ______________ промені спрямовані паралельно один одному і під кутом 90° до площини проекцій, то проектування називається ______________.
5. Натуральне зображення предмета на площині проекцій виходить лише за ______________ проектування.
6. Проекції розташовуються щодо один одного ______________________________.
7.Основоположником методу прямокутного проектування є _______________
Завдання 2. Дослідницький проект
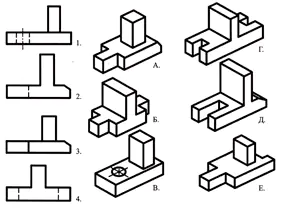
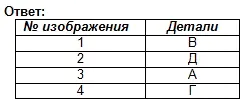
Встановіть відповідність основних видів, позначених цифрами, деталями, позначеними літерами, та запишіть відповідь у зошиті.
Вправа на повторення знань геометричних тіл.
За словесним описом знайти наочне зображення деталі.
Основа деталі має форму прямокутного паралелепіпеда, у менших гранях якого виконані пази, що мають форму правильної чотирикутної призми. У центрі верхньої грані паралелепіпеда розташований усічений конус, уздовж осі якого проходить наскрізний циліндричний отвір.
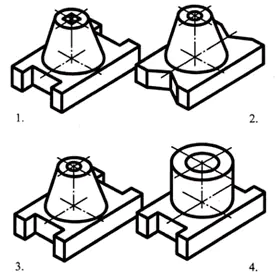
Відповідь: деталь №3 (1 бал)
Знайдіть відповідність технічних малюнків деталей та їх фронтальних проекцій (напрямок проектування позначено стрілкою). За розрізненими зображеннями креслення складіть креслення кожної деталі, що складається з трьох зображень. Відповідь запишіть до таблиці (рис. 129).
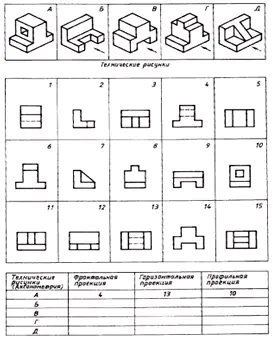
| Технічні малюнки | Фронтальна проекція | Горизонтальна проекція | Профільна проекція |
| А | 4 | 13 | 10 |
| Б | 12 | 9 | 2 |
| У | 14 | 5 | 1 |
| Г | 6 | 15 | 8 |
| Д | 11 | 3 | 7 |
ІІІ. Практична робота.
Завдання №1. Дослідницький проект
Знайдіть фронтальну та горизонтальну проекції до цього наочного зображення. Записати відповідь у зошит.
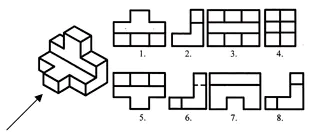
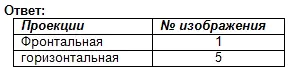
Оцінювання роботи на уроці. Самоперевірка. (Презентація 2)
На дошці записані бали для оцінювання першої частини роботи:
Завдання №2. Творча робота та перевірка його виконання
(Творчий проект)
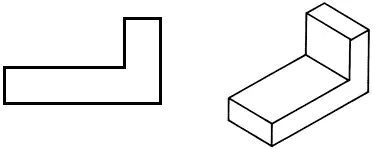
• Перекреслити передню проекцію в робочий зошит.
• Докреслити горизонтальну проекцію, змінивши форму деталі для зменшення її маси.
• За необхідності внести зміни на передній проекції.
• Для перевірки виконання завдання викликати одного-двох учнів до дошки з метою пояснення варіанта вирішення завдання.
IV. Підбиття підсумку уроку.
1. Оцінювання роботи на уроці. (Перевірка практичної частини роботи)
V. Завдання додому.
1. Дослідницький проект.
Робота за таблицею: визначити якого креслення, позначеного цифрою, відповідає малюнок, позначений буквою.
Частковий випадок паралельного проектування, при якому напрям проектування перпендикулярно площині проекцій, називається прямокутним або ортогональним проектуванням. Прямокутною (ортогональною) проекцією точки називають основу перпендикуляра, проведеного з точки на площину проекцій. Прямокутна проекція точок А та В показана на рис. 5.
Для визначення положення точки в просторі за її паралельними проекціями необхідно мати дві паралельні площини, отримані при двох напрямках проектування.
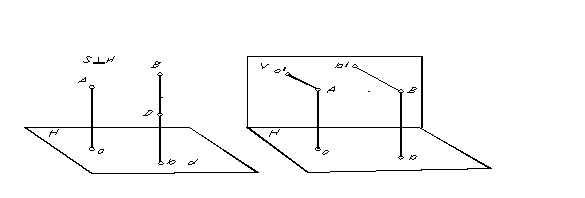 |
Т.к. через точку можна провести тільки одну пряму, перпендикулярну до площини, то, очевидно, при ортогональному проектуванні для отримання двох проекцій однієї точки необхідно мати дві не паралельні площині проекцій (рис. 6).
Ортогональне проектування має низку переваг перед центральним і паралельним проектуванням. До них насамперед слід віднести:
1. Простоту графічних побудов визначення ортогональних проекцій точок.
2. Можливість за певних умов зберегти на проекціях форму і розміри фігури, що проектується.
Зазначені переваги забезпечили широке застосування ортогонального проектування в техніці, зокрема для складання машинобудівних креслень.
У машинобудуванні для того щоб мати можливість за кресленням судити про форму і розміри предметів, що зображуються, при складанні креслень, як правило, користуються не двома, а декількома площинами проекцій.
Положення точки у просторі, отже, і будь-який геометричної фігури може бути визначено, якщо буде задана будь-яка координатна система віднесення. Площини проекції поділяють місце на вісім частин - октантів. Їх умовно нумерують римськими цифрами (рис. 7).
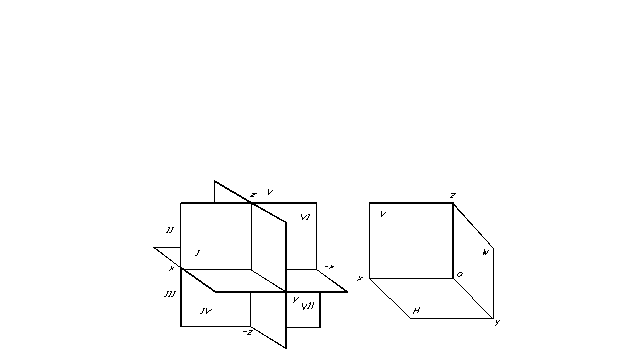
Площини проекції поділяють місце на вісім частин - октантів. Їх умовно нумерують римськими цифрами (рис. 7).
Найбільш зручною для фіксування положення геометричної фігури у просторі та виявлення її форми по ортогональних проекціях є декартова система координат, що складається з трьох взаємно перпендикулярних площин проекцій. У зв'язку з тим, що нарисна геометрія покликана передавати результати своїх теоретичних досліджень для практичного використання, ортогональне проектування доцільно розглядати також у системі трьох площин проекцій.
Для зручності проектування як три площини проекцій вибирають три взаємно перпендикулярні площини (рис.8). Одну з них прийнято розташовувати горизонтально - її називають горизонтальною площиною проекцій, іншу – вертикально, паралельно площині креслення, її називають фронтальною площиною проекцій і третю, перпендикулярну двом наявним – її називають профільною площиною проекцій. Ці площини проекцій перетинаються лініями, званими осями проекцій
У нас прийнято праву систему розташування площин проекцій. При цьому позитивними напрямками осей вважають: для осі х (перетин горизонтальної та фронтальної площин проекцій) – ліворуч від початку координат, для осі y (перетин горизонтальної та профільної площин проекцій) – у бік спостерігача від фронтальної площини проекцій, для осі z (перетин фронтальної та профільної площин проекцій) – вгору від горизонтальної площини проекцій, протилежні напрямок осей вважають негативними.
Проекцією точки є основа перпендикуляра, опущеного з точки відповідну площину проекцій. Горизонтальною проекцією точки називають прямокутну проекцію точки на горизонтальній площині проекцій, фронтальною проекцією – відповідно на фронтальній площині проекцій та профільний – на профільній поверхні проекцій.
Користуватися цим просторовим макетом для зображення ортогональних проекцій геометричних фігур незручно через його громіздкість, а також через те, що на окремих (горизонтальній та профільній) відбувається спотворення форми та розмірів фігури, що проектується. Тому замість зображення на кресленні просторового макета користуються комплексним кресленням (епюр Монжа), що складається з трьох пов'язаних між собою ортогональних проекцій геометричної фігури.
Перетворення просторового макета в епюр здійснюється шляхом поєднання горизонтальної та профільної площин проекцій з фронтальною площиною проекції (рис. 7).
Так як площини не мають меж, у суміщеному положенні (на епюрі) межі площин не показують, немає необхідності залишати написи, що вказують положення площин проекцій (рис. 10).
Перейшовши до епюру втратилася просторова наочність. Епюр дає більше - точність і зручність зображень, при простоті побудов. Проте, щоб уявити просторову картину потрібна робота уяви.
Чи не знайшли те, що шукали? Скористайтеся пошуком:
Найкращі вислови: Для студента найголовніше не скласти іспит, а вчасно згадати про нього. 9744 - | 7364 - або читати все.
Проекційне креслення (основи накреслювальної геометрії)
Метод проекцій
Спосіб прямокутного проектування
Якщо проецірующие промені становлять із площиною проекцій прямий кут, такі проекції називають прямокутними.
Прямокутні проекції називають також ортогональними. Слово "ортогональні" походить від грецьких слів "ortos" - прямий і "gonia" - кут.
Креслення у системі прямокутних проекцій дають повне уявлення про форму та розміри предмета. Їх легше виконувати, ніж аксонометричні проекції.
Що потрібно знати для успішного виконання креслень?
Будь-який предмет, що має плоскі поверхні, обмежується вершинами, ребрами та гранями (рис. 108). Отже, щоб навчитися зображати на кресленнях різноманітні предмети, потрібно знати, як у прямокутних проекціях зображуються вершини (крапки), ребра (відрізки прямих ліній) та грані предметів (частини площини).
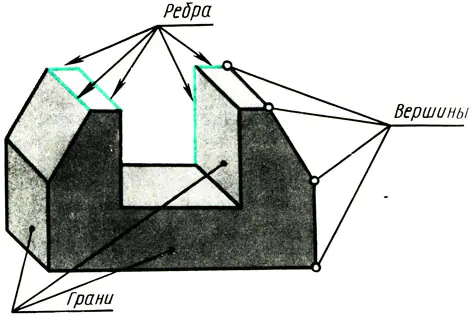
Мал. 108. Предмсч як сукупність точок, пиши. Вершини площин
Зробимо нескладний досвід. Простежимо, як зображуються у різних положеннях плоский предмет та сто елементи.
Приймемо протилежну вікну стіну за площину проекцій. Нехай із вікна перпендикулярно стіні падають промені світла - проецірующие промені. Розташуємо перед стіною (паралельно їй) аркуш щільного паперу ABCD (рис. 109, а). На стіні утворюється тінь, рівнозначна проекції предмета. Які її розміри? В даному випадку проекція a'b'c'd' за формою та розмірами відповідає об'єкту проектування — листу
ABCD. Спосіб проектування прямокутний, тому що проецірующие промені перпендикулярні площині проекцій.
Як буде змінюватися проекція, якщо зображуваний предмет повертатиме, наприклад, навколо його висоти — ребра AD (рис. 109, б)?
При повороті тінь скорочуватиметься по ширині (лінії а'b' і c'd' на рис. 109 б стають коротшими). Продовжуючи повертати аркуш паперу, зауважимо, що у положенні, перпендикулярному до стіни, зображення аркуша перетвориться на лінію (рис. 109, в), але висота предмета залишається постійною, тобто лінії a'd' і b'с' по довжині не спотворюються.
Тепер сформулюємо висновки про те, які зображення за формою та розмірами має у прямокутних проекціях плоский предмет, по-різному розташований по відношенню до площини проекцій :
а) плоска фігура, паралельна до площини проекцій, зображується на ній у натуральну величину (рис. 109, а);
б) плоска фігура, похильна до площини проекцій, зображується на ній зі спотворенням розмірів (рис. 109, б);
в) плоска фігура перпендикулярна до площини проекцій зображується на ній у вигляді відрізка прямої (рис. 109, в).
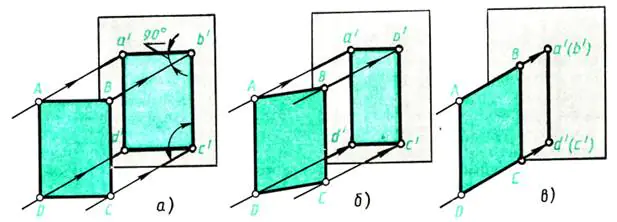
Мал. 109. Проеціювання плоскої фігури
Ці висновки належать до зображення граней предметів.
Як у прямокутних проекціях зображуються ребра предметів, т. е. лінії?
Повторимо досвід із поворотом плоского предмета, поспостерігаємо за тим, як проектуються його ребра, тобто лінії, і зробимо висновки:
а) відрізок прямої, паралельний площині проекцій, зображується на ній у натуральну величину (порівняйте висоту предмета AD і ВС на рис. 109, а, б, з її проекціями a'd' і b'с, а ширину предмета АВ і CD з її проекціями а'b' та c'd' на рис.109, а);
б) відрізок прямий, похилий до площини проекцій, зображується на ній зі спотворенням по довжині (порівняйте ширину предмета АВ і CD на рис. 109, б з її проекціями а'b' і c'd');
в) відрізок прямий, перпендикулярний до площини проекцій, зображується на ній точкою (див. на рис. 109, ширину предмета — лінії АВ і CD, перпендикулярні до площини проекцій).
Проекцією точки є основа перпендикуляра, опущеного з цієї точки в просторі на площину проекцій (див. точки а', b', с', d' - проекції точок А, В, С, D).
Умовимося точки в просторі позначати великими літерами А, В, С, D і т. д., а проекції точок - відповідними малими літерами я, Ь, с, d і т. д.
З двох точок, що збігаються на кресленні (рис. 109, в) одна є зображенням видимої вершини, а інша — невидимої (закритої). Позначення проекцій невидимих вершин беруть у дужки.



