Szakaszok: Technológia
Az óra céljai és céljai:
nevelési: mutasd meg a tanulóknak, hogyan használják a téglalap vetítési módszert rajzkészítés során;
• három vetítési sík használatának szükségessége;
• feltételek megteremtése a készségek kialakulásához, hogy egy tárgyat három vetületi síkra vetítsünk;
fejlesztés: fejlessze a tanulók térfogalmát, térbeli gondolkodását, kognitív érdeklődését és kreatív képességeit;
oktatás: felelősségteljes hozzáállás a rajzhoz, a grafikai munkakultúra ápolása.
A tanítás módszerei, technikái: magyarázat, beszélgetés, problémahelyzetek, kutatás, gyakorlatok, frontális munka az osztállyal, kreatív munka.
Anyagi támogatás: számítógépek, prezentáció „Téglalap vetítés”, feladatok, gyakorlatok, gyakorlatkártyák, prezentáció önellenőrzéshez.
Az óra típusa: lecke az ismeretek megszilárdítására.
Szókincsmunka: vízszintes sík, vetítés, vetítés, profil, kutatás, projekt.
I. Szervezeti rész.
Mondja el az óra témáját és célját!
Hajtsuk végre lecke-verseny, minden feladatért bizonyos számú pontot kapsz. Az elért pontok függvényében osztályzatot adunk a leckéhez.
II. A vetítés és típusainak áttekintése.
A kivetítés az a mentális folyamat, amelynek során tárgyi képeket készítünk síkon.
Az ismétlés prezentáció segítségével történik.
1. Diákokat kérdeznek problémás helyzet. (1. bemutató)
Elemezze az alkatrész geometriai alakját az elülső vetületen, és keresse meg ezt a részt a vizuális képek között.

Ebből a helyzetből azt a következtetést vonhatjuk le, hogy mind a 6 résznek ugyanaz a frontális vetülete. Ez azt jelenti, hogy egy vetítés nem mindig ad teljes képet az alkatrész alakjáról és kialakításáról.
- Mi a kiút ebből a helyzetből? (Nézd meg a részt a másik oldalról).
2. Szükség volt egy másik vetítési síkra. (Vízszintes vetítés).
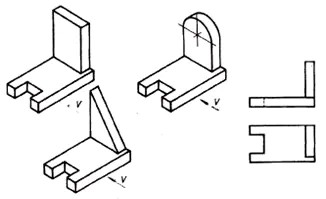
3. Harmadik vetítés szükségessége akkor merül fel, ha két vetület nem elegendő egy tárgy alakjának meghatározásához.
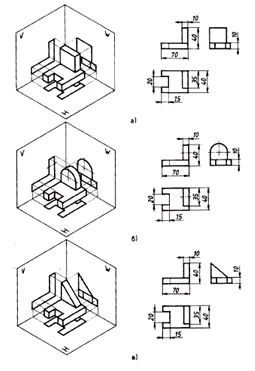
Méretezés:
- a frontális vetületen –
Következtetés: ez azt jelenti, hogy ahhoz, hogy megtanuljon rajzokat készíteni, képesnek kell lennie objektumokat síkra vetíteni.
Pótold a hiányzó szavakat a meghatározás szövegében!
1. Van _______________ és __________________ vetület.
2. Ha egy pontból ______________ sugár jön ki, a vetítést __________________-nak nevezzük.
3. Ha __________________ sugarak párhuzamosak, a vetítést _____________-nak nevezzük.
4. Ha ______________ sugarak egymással párhuzamosan és a vetítési síkkal 90°-os szöget zárnak be, akkor a vetületet __________________-nak nevezzük.
5. Egy objektum természetes képe egy vetítési síkon csak ______________ vetítéssel érhető el.
6. A vetületek egymáshoz képest ____________________________________
7. A téglalap vetítési módszer alapítója _______________
2. feladat Kutatási projekt
Párosítsa a számokkal jelölt fő típusokat a betűkkel jelölt részekkel, és írja le a választ a füzetébe!
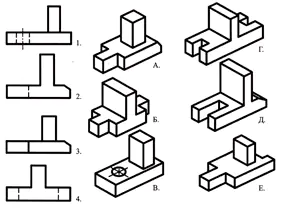
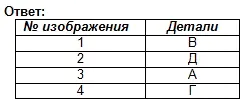
Gyakorlat a geometriai testekkel kapcsolatos ismeretek áttekintésére.
A szóbeli leírás segítségével keresse meg az alkatrész vizuális képét.
Az alkatrész alapja téglalap alakú paralelepipedon alakú, melynek kisebb oldalain szabályos négyszögű prizma alakú hornyok vannak. A paralelepipedon felső felületének közepén egy csonka kúp található, melynek tengelye mentén egy átmenő hengeres furat található.
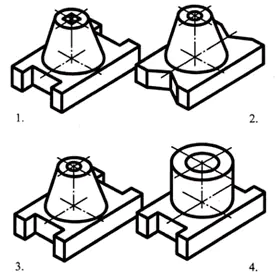
Válasz: 3. rész (1 pont)
Keresse meg az egyezést az alkatrészek műszaki rajzai és frontális vetületei között (a vetítés irányát nyíllal jelöljük). A rajz elszórt képei alapján készíts minden részről rajzot, amely három képből áll. Válaszát írja be a táblázatba (129. ábra).
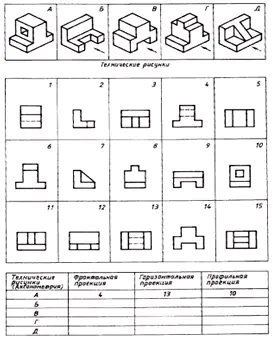
| Műszaki rajzok | Frontális vetítés | Vízszintes vetítés | Profilvetítés |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| BAN BEN | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktikus munka.
1. számú feladat. Kutatási projekt
Keresse meg ennek a vizuális képnek a frontális és vízszintes vetületeit. Írd le a választ a füzetedbe.
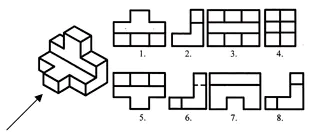
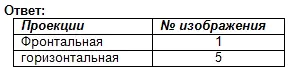
Munka értékelése az órán. Önteszt. (2. bemutató)
A munka első részének osztályozási pontjait fel kell írni a táblára:
2. feladat. Alkotó munka és megvalósításának ellenőrzése
(kreatív projekt)
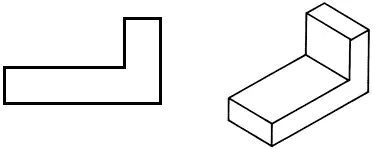
• Rajzolja be a frontális vetületet a munkafüzetébe.
• Rajzoljon vízszintes vetületet, megváltoztatva az alkatrész alakját a tömegének csökkentése érdekében.
• Ha szükséges, módosítsa a frontális vetületet.
• A feladat elvégzésének ellenőrzéséhez hívj egy vagy két tanulót a táblához, hogy magyarázzák el a probléma megoldását.
IV. Összegezve a tanulságot.
1. Az órán végzett munka értékelése. (A munka gyakorlati részének ellenőrzése)
V. Házi feladat.
1. Kutatási projekt.
Dolgozzon a táblázat szerint: határozza meg, hogy melyik számmal jelölt rajz felel meg a betűvel jelölt rajznak.
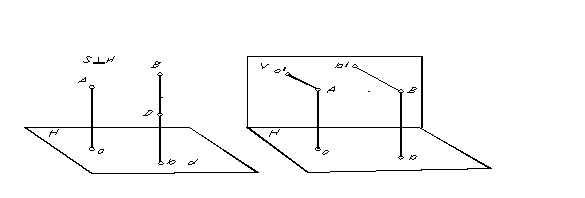
A párhuzamos vetítés egy speciális esete, amelyben a vetítés iránya merőleges a vetítési síkra, ún. négyszögletes vagy ortogonális vetület. Egy pont derékszögű (merőleges) vetülete a pontból a vetítési síkra húzott merőleges alapja. Az A és B pont téglalap vetületét a ábra mutatja. 5.
Egy pont térbeli helyzetének meghatározásához a párhuzamos vetületeiből két párhuzamos síkra van szükség, amelyeket két vetítési irányban kapunk.
 |
Mert ponton keresztül csak egy, a síkra merőleges egyenes húzható, ekkor nyilvánvalóan merőleges vetítéssel, hogy egy pont két vetületét kapjuk, két nem párhuzamos vetítési síkra van szükség (6. ábra). .
Az ortográfiai vetítésnek számos előnye van a központi és párhuzamos vetítéssel szemben. Ezek elsősorban a következőket tartalmazzák:
1. Grafikus konstrukciók egyszerűsége pontok ortogonális vetületeinek meghatározásához.
2. A vetített alak alakjának és méretének a vetületeken való megőrzésének képessége bizonyos feltételek mellett.
A megemlített előnyök biztosították az ortogonális vetítés széleskörű elterjedését a technológiában, különösen a gépészeti rajzok elkészítésében.
A gépészetben annak érdekében, hogy rajz alapján meg lehessen ítélni az ábrázolt tárgyak alakját és méretét, a rajzok készítésekor általában nem két, hanem több vetületi síkot használnak.
Egy pont helye a térben, tehát bármely geometriai alakzat, meghatározható, ha bármilyen koordináta-referenciarendszert megadunk. A vetületi síkok nyolc részre osztják a teret - oktánsra. Hagyományosan római számokkal vannak számozva (7. ábra).
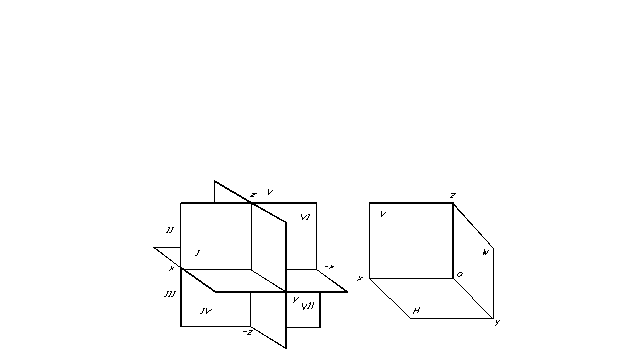
A vetületi síkok nyolc részre osztják a teret - oktánsra. Hagyományosan római számokkal vannak számozva (7. ábra).
A geometriai alakzat térbeli helyzetének rögzítésére és alakjának ortogonális vetületekből történő azonosítására a legkényelmesebb a Descartes-féle koordinátarendszer, amely három egymásra merőleges vetületi síkból áll. Tekintettel arra, hogy a leíró geometria elméleti kutatásának eredményeit gyakorlati felhasználásra hivatott közvetíteni, célszerű az ortogonális vetítést három vetületi sík rendszerében is figyelembe venni.
A vetítés megkönnyítése érdekében három egymásra merőleges síkot választunk három vetítési síknak (8. ábra). Az egyiket általában vízszintesen helyezik el - úgy hívják vízszintes vetítési sík, a másik függőleges, párhuzamos a rajzsíkkal, úgy hívják a vetületek frontális síkja egy harmadik pedig a két meglévőre merőlegesen – úgy hívják a vetületek profilsíkja. Ezek a vetületi síkok metszik egymást az ún vetítési tengelyek.
A vetítési síkok elrendezésére jobbkezes rendszert alkalmaztunk. Ebben az esetben a tengelyek pozitív irányait veszik figyelembe: a tengelyre x (vízszintes és frontális vetítési síkok metszéspontja) – az origótól balra, a tengelyre y (vízszintes és profilvetítési síkok metszéspontja) – a frontális vetítési síkról a megfigyelő felé, a tengelyre z (a vetületek homlok- és profilsíkjainak metszéspontja) – a vetületek vízszintes síkjából felfelé a tengelyek ellentétes irányai negatívnak számítanak.
Egy pont vetülete a pontból a megfelelő vetítési síkra húzott merőleges alapja. Vízszintes vetítés a pontok egy pont téglalap alakú vetületei egy vízszintes vetítési síkon, frontális vetítés – illetve a vetületek frontális síkján, ill profil – a vetületek profilsíkján.
Ezt a térbeli elrendezést kényelmetlen geometriai alakzatok merőleges vetületeinek ábrázolására használni terjedelmessége miatt, valamint azért is, mert az egyes alakzatokon (vízszintes és profil) a vetített alak alakja és mérete torzul. Ezért ahelyett, hogy egy térbeli elrendezést rajzon ábrázolnának, egy összetett rajzot (Monge diagram) használnak, amely egy geometriai alakzat három egymáshoz kapcsolódó, merőleges vetületéből áll.
A térbeli elrendezés diagramokká alakítása a vízszintes és a profilvetítési síkok és a frontális vetítési sík kombinálásával történik (7. ábra).
Mivel a síkoknak nincs határa, a kombinált helyzetben (a diagramon) a síkok határai nem láthatók, nem kell a vetítési síkok helyzetét jelző feliratokat hagyni (10. ábra).
A diagramra váltva a térbeli tisztaság elveszett. A diagram többet ad - a képek pontosságát és könnyű mérését az egyszerű felépítés mellett. Egy térbeli kép elképzeléséhez azonban a képzelet munkája szükséges.
Nem találta meg, amit keresett? Használd a keresőt:
A legjobb mondások: Egy diák számára nem az a legfontosabb, hogy sikeres legyen a vizsga, hanem hogy időben emlékezzen rá. 9744 — | 7364 - vagy olvassa el az összeset.
Vetítési rajz (a leíró geometria alapjai)
Vetítési módszer
Téglalap vetítési módszer
Ha a vetületi sugarak derékszöget zárnak be a vetítési síkkal, akkor az ilyen vetületeket nevezzük négyszögletes.
Négyszögletes vetületeket is neveznek ortogonális. Az "ortogonális" szó a görög "ortos" - egyenes és "gonia" - szög szavakból származik.
A téglalap alakú vetületek rendszerében készült rajzok teljes képet adnak a tárgy alakjáról és méretéről. Könnyebben kivitelezhetők, mint az axonometrikus vetítések.
Mit kell tudni a rajzok sikeres elkészítéséhez?
Minden sík felületű objektumot csúcsok, élek és lapok korlátoznak (108. ábra). Ezért a különféle objektumok rajzokon való ábrázolásának megtanulásához tudnia kell, hogy a csúcsok (pontok), az élek (egyenesek szakaszai) és az objektumok élei (sík részei) hogyan jelennek meg a téglalap alakú vetületekben.
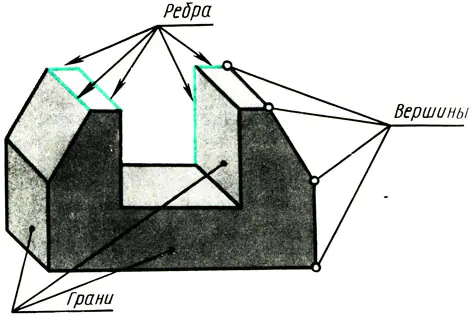
Rizs. 108. Premsch mint ponthalmaz, írd. Síkok csúcsai
Végezzünk egy egyszerű kísérletet. Nézzük meg, hogyan ábrázolják különböző pozíciókban egy lapos tárgyat és száz elemet.
Vegyük az ablakkal szemközti falat vetítési síknak. Engedd ki az ablakon merőleges Fénysugarak esnek a falra – kivetülő sugarak. Helyezzen egy vastag ABCD papírlapot a fal elé (vele párhuzamosan) (109. ábra, a). A falon egy árnyék keletkezik, amely megfelel a tárgy vetületének. Mik a méretei? Ebben az esetben az a’b’c’d vetület alakjában és méretében megfelel a vetítés tárgyának - a lapnak
ABCD. A vetítési módszer téglalap alakú, mivel a vetületi sugarak merőlegesek a vetítési síkra.
Hogyan változik a vetület, ha az ábrázolt objektumot elforgatjuk, például a magassága körül – AD éle (109. ábra, b)?
Forduláskor az árnyék szélességében zsugorodni fog (a 109. ábrán az a’b’ és c’d’ vonal, a b rövidül). Folytatva a papírlap forgatását, megjegyezzük, hogy a falra merőleges helyzetben a lap képe vonallá változik (109. ábra, c), de a tárgy magassága állandó marad, azaz a' vonalak. d' és b'c' a hossz mentén nem torzul.
Most fogalmazzunk meg következtetéseket arról, hogy egy sík tárgynak milyen alakú és méretű képei vannak téglalap alakú vetületekben, amelyek a vetítési síkhoz képest eltérően helyezkednek el:
a) a vetítési síkkal párhuzamos lapos alakot ábrázolunk rajta természetes méretben (109. ábra, a);
b) egy, a vetítési síkhoz hajló lapos alakot ábrázolnak rajta mérettorzítással (109. ábra, b);
c) a vetítési síkra merőleges lapos alakot ábrázolunk rajta egyenes szakasz formájában (109. ábra, c).
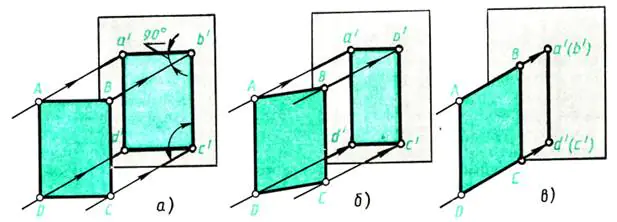
Rizs. 109. Lapos figura kivetítése
Ezek a megállapítások a tárgyak széleinek ábrázolására vonatkoznak.
Hogyan ábrázolják az objektumok éleit, azaz a vonalakat téglalap alakú vetületekben?
Ismételjük meg a kísérletet egy lapos tárgy elforgatásával, figyeljük meg, hogyan vetülnek ki élei, azaz vonalai, és vonjunk le következtetéseket:
a) természetes méretben ábrázoljuk rajta a vetítési síkkal párhuzamos egyenes szakaszt (hasonlítsuk össze a 109. ábra AD és BC objektumának magasságát a, b, c a'd' és b'c vetületeivel, valamint az AB és CD objektum szélessége a'b' és c'd' vetületeivel a 109. ábrán, a);
b) a vetítési síkra hajló egyenes szakaszt ábrázolunk hosszában torzulva (hasonlítsuk össze a 109. ábrán látható AB és CD tárgy szélességét, b a’b’ és c’d’ vetületeivel);
c) a vetítési síkra merőleges egyenes szakaszt egy pont ábrázolja rajta (lásd a 109. ábrát az objektum szélességében - AB és CD egyenesek, merőlegesek a vetítési síkra).
Egy pont vetülete a tér adott pontjából a vetítési síkra süllyesztett merőleges alapja (lásd a’, b’, c’, d’ pontok - A, B, C, D pontok vetületei).
Állapodjunk meg abban, hogy a térben lévő pontokat nagybetűkkel A, B, C, D stb., a pontok vetületeit a megfelelő kisbetűkkel i, b, c, d stb. jelöljük.
A rajzon (109. ábra, c) egybeeső két pont közül az egyik egy látható csúcs képe, a másik pedig egy láthatatlan (zárt) pont. A láthatatlan csúcsok vetületeinek jelölése zárójelben van.



