Раздели: технология
Цели и задачи на урока:
образователен: покажете на учениците как да използват метода на правоъгълна проекция, когато правят чертеж;
• необходимостта от използване на три проекционни равнини;
• създават условия за формиране на умения за проектиране на обект върху три проекционни равнини;
развитие: развиват пространствени концепции, пространствено мислене, познавателен интерес и творчески способности на учениците;
възпитаване: отговорно отношение към рисуването, да се култивира култура на графична работа.
Методи и техники на обучение: обяснение, разговор, проблемни ситуации, изследване, упражнения, фронтална работа с класа, творческа работа.
Материална подкрепа: компютри, презентация „Правоъгълна проекция”, задачи, упражнения, карти с упражнения, презентация за самопроверка.
Тип урок: урок за консолидиране на знанията.
Речникова работа: хоризонтална равнина, проекция, проекция, профил, изследване, проект.
I. Организационна част.
Посочете темата и целта на урока.
Нека изпълним урок-състезание, за всяка задача ще получите определен брой точки. В зависимост от събраните точки ще бъде поставена оценка за урока.
II. Преглед на проекцията и нейните видове.
Проекцията е умствен процес на конструиране на изображения на обекти в равнина.
Повторението се извършва с помощта на презентация.
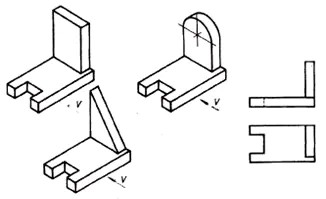
1. Питат се учениците проблемна ситуация. (Презентация 1)
Анализирайте геометричната форма на частта на предната проекция и намерете тази част сред визуалните изображения.

От тази ситуация се заключава, че всичките 6 части имат една и съща фронтална проекция. Това означава, че една проекция не винаги дава пълна картина на формата и дизайна на детайла.
- Какъв е изходът от тази ситуация? (Погледнете частта от другата страна).
2. Имаше нужда да се използва друга проекционна равнина. (Хоризонтална проекция).
3. Необходимостта от трета проекция възниква, когато две проекции не са достатъчни, за да се определи формата на даден обект.
Размер:
- на предната проекция -
Заключение: това означава, че за да се научите как да правите чертежи, трябва да можете да проектирате обекти върху равнина.
Попълнете пропуснатите думи в текста на дефиницията.
1. Има _______________ и ______________ проекция.
2. Ако ______________ лъчи излизат от една точка, проекцията се нарича ______________.
3. Ако ______________ лъчите са насочени успоредно, проекцията се нарича _____________.
4. Ако ______________ лъчите са насочени успоредно един на друг и под ъгъл от 90 ° спрямо равнината на проекцията, тогава проекцията се нарича ______________.
5. Естествено изображение на обект върху проекционна равнина се получава само с ______________ проекция.
6. Проекциите са разположени една спрямо друга__________________________.
7. Основателят на метода на правоъгълната проекция е _______________
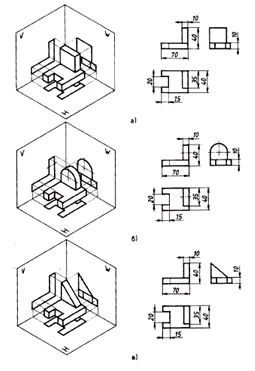
Задача 2. Изследователски проект
Свържете основните типове, обозначени с цифри, с частите, обозначени с букви, и запишете отговора в тетрадката си.
Упражнение за повторение на знанията за геометрични тела.
Използвайки словесното описание, намерете визуално изображение на частта.
Основата на детайла има формата на правоъгълен паралелепипед, по-малките лица на който имат канали във формата на правилна четириъгълна призма. В центъра на горната страна на паралелепипеда има пресечен конус, по оста на който има проходен цилиндричен отвор.
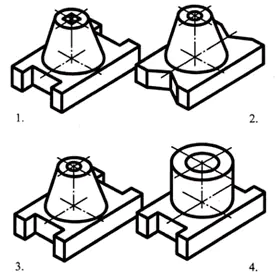
Отговор: част No3 (1 точка)
Намерете съответствието между техническите чертежи на частите и техните челни проекции (посоката на проекцията е отбелязана със стрелка). Въз основа на разпръснатите изображения на чертежа направете чертеж на всяка част, състоящ се от три изображения. Запишете отговора си в таблицата (фиг. 129).
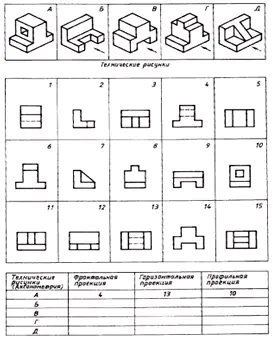
| Технически чертежи | Фронтална проекция | Хоризонтална проекция | Профилна проекция |
| А | 4 | 13 | 10 |
| б | 12 | 9 | 2 |
| IN | 14 | 5 | 1 |
| Ж | 6 | 15 | 8 |
| д | 11 | 3 | 7 |
III. Практическа работа.
Задача No1. Изследователски проект
Намерете фронталната и хоризонталната проекции за това визуално изображение. Запишете отговора в тетрадката си.
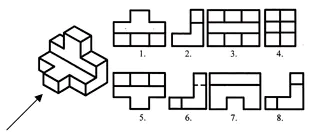
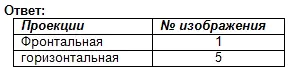
Оценка на работата в урока. Самотест. (Презентация 2)
Точките за оценяване на първата част от работата са записани на дъската:
Задача No2. Творческа работа и проверка на нейното изпълнение
(творчески проект)
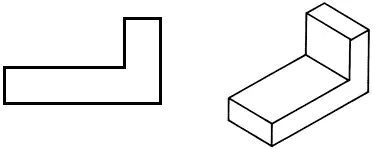
• Начертайте челната проекция в работната си тетрадка.
• Начертайте хоризонтална проекция, променяйки формата на детайла, за да намалите масата му.
• Ако е необходимо, направете промени във фронталната проекция.
• За да проверите изпълнението на задачата, извикайте един или двама ученика на дъската, за да обяснят своето решение на задачата.
IV. Обобщаване на урока.
1. Оценка на работата в урока. (Проверка на практическата част от работата)
V. Задаване на домашна работа.
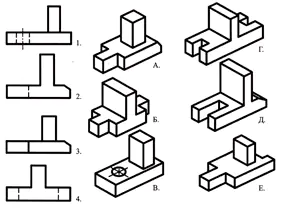
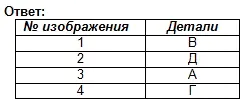
1. Изследователски проект.
Работете по таблицата: определете кой чертеж, означен с цифра, съответства на чертежа, означен с буква.
Специален случай на успоредно проектиране, при който посоката на проектиране е перпендикулярна на проекционната равнина, се нарича правоъгълен или ортогонална проекция. Правоъгълната (ортогонална) проекция на точка е основата на перпендикуляра, прекаран от точката към проекционната равнина. Правоъгълната проекция на точки A и B е показана на фиг. 5.
За да се определи позицията на точка в пространството от нейните успоредни проекции, е необходимо да има две успоредни равнини, получени в две посоки на проекцията.
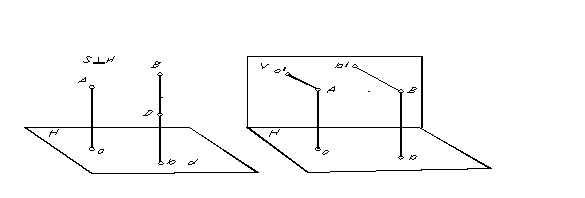 |
Защото през точка може да се начертае само една права линия, перпендикулярна на равнината, тогава, очевидно, с ортогонална проекция, за да се получат две проекции на една точка, е необходимо да има две непаралелни проекционни равнини (фиг. 6) .
Ортографската проекция има редица предимства пред централната и паралелната проекция. Те включват предимно:
1. Простота на графичните конструкции за определяне на ортогонални проекции на точки.
2. Способността при определени условия да запази формата и размера на проектираната фигура върху проекциите.
Отбелязаните предимства са осигурили широкото използване на ортогонална проекция в технологиите, по-специално за изготвяне на чертежи на машиностроенето.
В машиностроенето, за да могат да преценят по чертеж формата и размера на изобразените обекти, при изготвянето на чертежи, като правило, използват не две, а няколко проекционни равнини.
Позицията на точка в пространството и следователно на всяка геометрична фигура може да се определи, ако е зададена произволна координатна референтна система. Проекционните равнини разделят пространството на осем части - октанти. Условно са номерирани с римски цифри (фиг. 7).
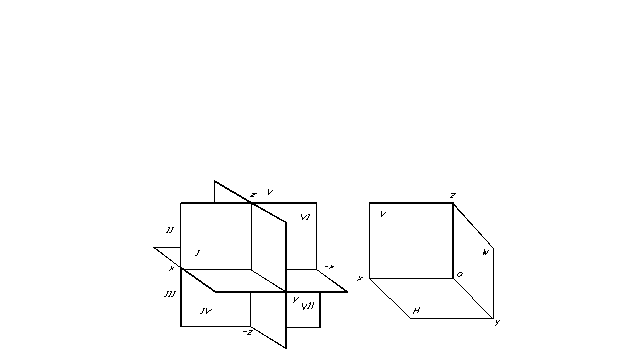
Проекционните равнини разделят пространството на осем части - октанти. Условно са номерирани с римски цифри (фиг. 7).
Най-удобната за фиксиране на позицията на геометрична фигура в пространството и идентифициране на нейната форма от ортогонални проекции е декартовата координатна система, състояща се от три взаимно перпендикулярни проекционни равнини. Поради факта, че дескриптивната геометрия е предназначена да предаде резултатите от своите теоретични изследвания за практическа употреба, препоръчително е да се разгледа ортогоналната проекция и в система от три проекционни равнини.
За по-лесно прожектиране три взаимно перпендикулярни равнини са избрани като три проекционни равнини (фиг. 8). Един от тях обикновено се поставя хоризонтално - т.нар хоризонтална проекционна равнина, другата е вертикална, успоредна на чертожната равнина, нарича се фронтална равнина на проекциите и трета, перпендикулярна на двете съществуващи - т.нар профилна равнина на проекциите. Тези проекционни равнини се пресичат по прави, наречени проекционни оси.
Приехме дясна система за подреждане на проекционни равнини. В този случай се разглеждат положителните посоки на осите: за ос х (пресечна точка на хоризонтална и фронтална проекционна равнина) – вляво от началото, за оста г (пресечна точка на хоризонтална и профилна проекционна равнина) – към наблюдателя от фронталната проекционна равнина, за ос z (пресичане на фронталната и профилната равнина на проекциите) - нагоре от хоризонталната равнина на проекциите противоположните посоки на осите се считат за отрицателни.
Проекцията на точка е основата на перпендикуляра, прекаран от точката върху съответната проекционна равнина. Хоризонтална проекция точките са правоъгълна проекция на точка върху хоризонтална проекционна равнина, фронтална проекция – съответно на фронталната равнина на проекциите и профил – върху профилната равнина на проекциите.
Използването на това пространствено оформление за изобразяване на ортогонални проекции на геометрични фигури е неудобно поради неговата обемност, а също и поради факта, че на отделни (хоризонтални и профилни) формата и размерът на проектираната фигура са изкривени. Следователно, вместо да изобразяват пространствено оформление в чертеж, те използват комплексен чертеж (диаграма на Монж), съставен от три взаимосвързани ортогонални проекции на геометрична фигура.
Преобразуването на пространственото оформление в диаграми се извършва чрез комбиниране на хоризонталните и профилните проекционни равнини с фронталната проекционна равнина (фиг. 7).
Тъй като равнините нямат граници, в комбинирано положение (на диаграмата) границите на равнините не се показват, не е необходимо да се оставят надписи, указващи положението на проекционните равнини (фиг. 10).
След като преминахте към диаграмата, пространствената яснота беше загубена. Диаграмата дава повече - точност и лекота на измерване на изображенията, с простота на конструкцията. Въпреки това, за да си представите пространствена картина, е необходима работа на въображението.
Не намерихте това, което търсихте? Използвайте търсачката:
Най-добрите думи: За студента най-важното е не да издържи изпита, а да си спомни за него навреме. 9744 — | 7364 - или прочетете всички.
Проекционен чертеж (основи на дескриптивната геометрия)
Проекционен метод
Метод на правоъгълна проекция
Ако проектиращите лъчи правят прав ъгъл с равнината на проекцията, тогава такива проекции се наричат правоъгълен.
Правоъгълни проекции също се наричат ортогонален. Думата "ортогонален" идва от гръцките думи "ortos" - прав и "gonia" - ъгъл.
Чертежите в системата на правоъгълните проекции дават пълна представа за формата и размера на обекта. Те са по-лесни за изпълнение от аксонометричните проекции.
Какво трябва да знаете, за да завършите успешно чертежите?
Всеки обект, който има плоски повърхности, е ограничен от върхове, ръбове и лица (фиг. 108). Следователно, за да научите как да изобразявате различни обекти на чертежи, трябва да знаете как върховете (точки), ръбовете (сегменти от прави линии) и ръбовете на обекти (части от равнина) са изобразени в правоъгълни проекции.
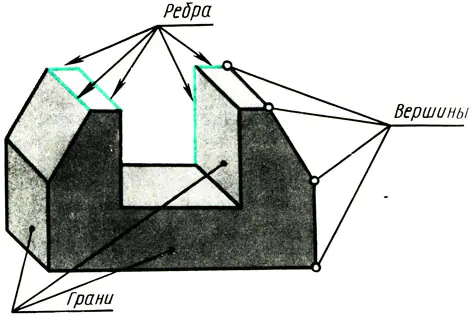
Ориз. 108. Премш като набор от точки, напишете. Върхове на равнини
Нека направим един прост експеримент. Нека да видим как са изобразени плосък обект и сто елемента в различни позиции.
Нека вземем стената срещу прозореца като проекционна равнина. Пусни го през прозореца перпендикулярен Светлинни лъчи падат върху стената - проектиращи лъчи. Поставете лист дебела хартия ABCD пред стената (успоредно на нея) (фиг. 109, а). На стената се образува сянка, еквивалентна на проекцията на обекта. Какви са размерите му? В този случай проекцията a’b’c’d’ съответства по форма и размер на обекта на проекция – листа
ABCD. Методът на проекция е правоъгълен, тъй като проектиращите лъчи са перпендикулярни на равнината на проекцията.
Как ще се промени проекцията, ако изобразеният обект се завърти, например, около неговата височина - ръб AD (фиг. 109, b)?
При завъртане сянката ще се свие по ширина (линиите a’b’ и c’d’ на фиг. 109, b стават по-къси). Продължавайки да завъртаме листа хартия, отбелязваме, че в позиция, перпендикулярна на стената, изображението на листа ще се превърне в линия (фиг. 109, c), но височината на обекта остава постоянна, т.е. линии a' d' и b'c' по дължината не са изкривени.
Сега нека формулираме изводи за това каква форма и размер има изображения на плосък обект в правоъгълни проекции, различно разположени спрямо равнината на проекцията:
а) върху нея в естествен размер е изобразена плоска фигура, успоредна на проекционната равнина (фиг. 109, а);
б) върху нея е изобразена плоска фигура, наклонена към проекционната равнина, с изкривяване на размерите (фиг. 109, б);
в) върху него е изобразена плоска фигура, перпендикулярна на проекционната равнина, под формата на прав сегмент (фиг. 109, в).
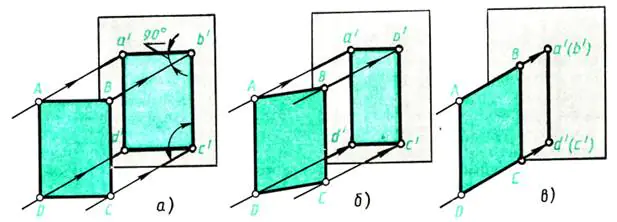
Ориз. 109. Проектиране на плоска фигура
Тези находки се отнасят до изобразяването на ръбовете на предметите.
Как се изобразяват ръбовете на обекти, т.е. линии, в правоъгълни проекции?
Нека повторим експеримента с въртене на плосък обект, да наблюдаваме как се проектират неговите ръбове, т.е. линии, и да направим изводи:
а) върху него е изобразен сегмент от права линия, успореден на проекционната равнина, в естествен размер (сравнете височината на обекта AD и BC на фиг. 109, a, b, c с неговите проекции a'd' и b'c, и ширината на обекта AB и CD с неговите проекции a'b' и c'd' на фиг. 109, a);
б) прав сегмент, наклонен към равнината на проекцията, е изобразен върху него с изкривяване по дължина (сравнете ширината на обекта AB и CD на фиг. 109, b с неговите проекции a’b’ и c’d’);
в) отсечка от права линия, перпендикулярна на проекционната равнина, се изобразява с точка върху нея (вижте на фиг. 109, по ширината на обекта - линиите AB и CD, перпендикулярни на проекционната равнина).
Проекцията на точка е основата на перпендикуляр, спуснат от дадена точка в пространството върху проекционната равнина (виж точки a’, b’, c’, d’ - проекции на точки A, B, C, D).
Нека се съгласим точките в пространството да се обозначават с главни букви A, B, C, D и т.н., а проекциите на точките със съответните малки букви i, b, c, d и т.н.
От двете точки, съвпадащи на чертежа (фиг. 109, c), едната е изображение на видим връх, а другата е невидим (затворен). Обозначаването на проекции на невидими върхове е взето в скоби.



