Sezioni: Tecnologia
Scopi e obiettivi della lezione:
educativo: mostrare agli studenti come utilizzare il metodo della proiezione rettangolare quando si realizza un disegno;
• la necessità di utilizzare tre piani di proiezione;
• creare le condizioni per la formazione di abilità per proiettare un oggetto su tre piani di proiezione;
sviluppando: sviluppare concetti spaziali, pensiero spaziale, interesse cognitivo e capacità creative degli studenti;
educare: atteggiamento responsabile nei confronti del disegno, coltivare una cultura del lavoro grafico.
Metodi e tecniche di insegnamento: spiegazione, conversazione, situazioni problematiche, ricerca, esercitazioni, lavoro frontale con la classe, lavoro creativo.
Supporto materiale: computer, presentazione “Proiezione rettangolare”, compiti, esercizi, schede di esercizi, presentazione per autotest.
Tipologia di lezione: lezione per consolidare le conoscenze.
Lavoro sul vocabolario: piano orizzontale, proiezione, proiezione, profilo, ricerca, progetto.
I. Parte organizzativa.
Indica l'argomento e lo scopo della lezione.
Eseguiamo lezione-concorso, per ogni attività riceverai un certo numero di punti. A seconda del punteggio ottenuto verrà assegnato un voto alla lezione.
II. Ripetizione della proiezione e sue tipologie.
La proiezione è il processo mentale di costruzione di immagini di oggetti su un piano.
La ripetizione viene eseguita utilizzando la presentazione.
1. Si chiede agli studenti situazione problematica. (Presentazione 1)
Analizza la forma geometrica della parte sulla proiezione frontale e trova questa parte tra le immagini visive.

Da questa situazione si conclude che tutte e 6 le parti hanno la stessa proiezione frontale. Ciò significa che una proiezione non sempre fornisce un quadro completo della forma e del design della parte.
- Qual è la via d'uscita da questa situazione? (Guarda la parte dall'altro lato).
2. Era necessario utilizzare un altro piano di proiezione. (Proiezione orizzontale).
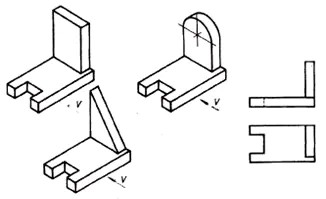
3. La necessità di una terza proiezione nasce quando due proiezioni non sono sufficienti per determinare la forma di un oggetto.
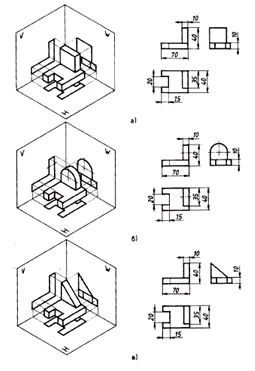
Dimensionamento:
- sulla proiezione frontale –
Conclusione: questo significa che per imparare a fare disegni è necessario saper proiettare gli oggetti su un piano.
Inserisci le parole mancanti nel testo della definizione.
1. Ci sono _______________ e ______________ proiezione.
2. Se da un punto escono ______________ raggi, la proiezione si chiama ______________.
3. Se i raggi ______________ sono diretti parallelamente, la proiezione è chiamata _____________.
4. Se i raggi ______________ sono diretti parallelamente tra loro e con un angolo di 90 ° rispetto al piano di proiezione, la proiezione viene chiamata ______________.
5. Un'immagine naturale di un oggetto su un piano di proiezione si ottiene solo con la proiezione ______________.
6. Le proiezioni sono posizionate l'una rispetto all'altra______________________________.
7. Il fondatore del metodo di proiezione rettangolare è _______________
Compito 2. Progetto di ricerca
Abbina le tipologie principali indicate dai numeri con le parti indicate dalle lettere e scrivi la risposta sul tuo quaderno.
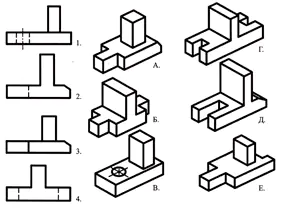
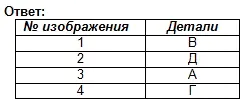
Un esercizio di ripasso della conoscenza dei corpi geometrici.
Utilizzando la descrizione verbale, trova un'immagine visiva della parte.
La base del pezzo ha la forma di un parallelepipedo rettangolare, le cui facce minori presentano scanalature a forma di prisma quadrangolare regolare. Al centro della faccia superiore del parallelepipedo è presente un tronco di cono, lungo l'asse del quale è presente un foro cilindrico passante.
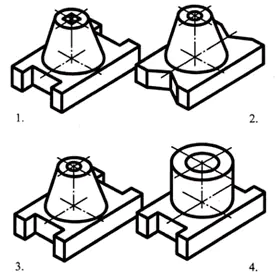
Risposta: parte n. 3 (1 punto)
Trovare la corrispondenza tra i disegni tecnici delle parti e le loro proiezioni frontali (la direzione di proiezione è contrassegnata da una freccia). Sulla base delle immagini sparse del disegno, crea un disegno di ciascuna parte, composto da tre immagini. Scrivi la tua risposta nella tabella (Fig. 129).
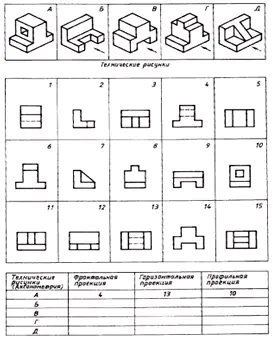
| Disegni tecnici | Proiezione frontale | Proiezione orizzontale | Proiezione del profilo |
| UN | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| IN | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Lavoro pratico.
Compito n. 1. Progetto di ricerca
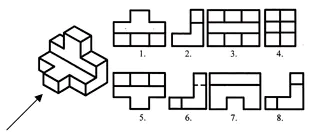
Trova le proiezioni frontale e orizzontale per questa immagine visiva. Scrivi la risposta sul tuo quaderno.
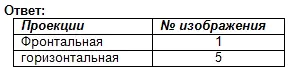
Valutazione del lavoro durante la lezione. Test di autoverifica. (Presentazione 2)
Alla lavagna sono scritti i punti per la valutazione della prima parte del lavoro:
Compito n. 2. Lavoro creativo e verifica della sua realizzazione
(progetto creativo)
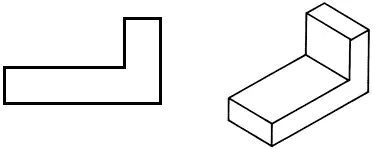
• Disegna la proiezione frontale nel tuo quaderno di esercizi.
• Disegnare una proiezione orizzontale, modificando la forma della parte per ridurne la massa.
• Se necessario, apportare modifiche alla proiezione frontale.
• Per verificare il completamento del compito, chiama uno o due studenti alla lavagna per spiegare la loro soluzione al problema.
IV. Riassumendo la lezione.
1. Valutazione del lavoro durante la lezione. (Verifica della parte pratica del lavoro)
V. Assegnazione dei compiti.
1. Progetto di ricerca.
Lavora secondo la tabella: determina quale disegno, contrassegnato da un numero, corrisponde al disegno, contrassegnato da una lettera.
Viene chiamato un caso speciale di proiezione parallela, in cui la direzione di proiezione è perpendicolare al piano di proiezione rettangolare O proiezione ortogonale. La proiezione rettangolare (ortogonale) di un punto è la base della perpendicolare tracciata dal punto al piano di proiezione. La proiezione rettangolare dei punti A e B è mostrata in Fig. 5.
Per determinare la posizione di un punto nello spazio dalle sue proiezioni parallele, è necessario disporre di due piani paralleli ricavati in due direzioni di proiezione.
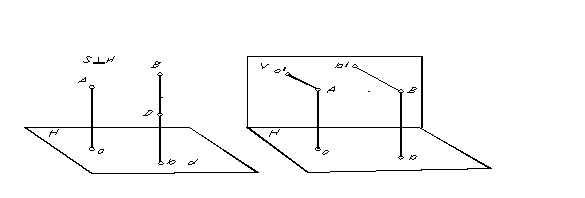 |
Perché per un punto si può tracciare una sola retta perpendicolare al piano, poi, ovviamente, con la proiezione ortogonale, per ottenere due proiezioni di un punto, è necessario avere due piani di proiezione non paralleli (Fig. 6) .
La proiezione ortografica presenta numerosi vantaggi rispetto alla proiezione centrale e parallela. Questi includono principalmente:
1. Semplicità delle costruzioni grafiche per determinare proiezioni ortogonali di punti.
2. La capacità, in determinate condizioni, di preservare la forma e le dimensioni della figura proiettata sulle proiezioni.
I vantaggi notati hanno assicurato l'uso diffuso della proiezione ortogonale nella tecnologia, in particolare, per la preparazione di disegni di ingegneria meccanica.
Nell'ingegneria meccanica, per poter giudicare da un disegno la forma e le dimensioni degli oggetti raffigurati, quando si redigono i disegni, di regola, si utilizzano non due, ma diversi piani di proiezione.
La posizione di un punto nello spazio, e quindi di qualsiasi figura geometrica, può essere determinata se viene specificato un qualsiasi sistema di riferimento di coordinate. I piani di proiezione dividono lo spazio in otto parti: ottanti. Sono convenzionalmente numerati con numeri romani (Fig. 7).
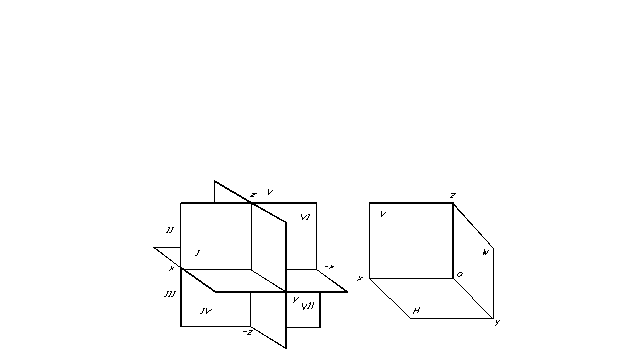
I piani di proiezione dividono lo spazio in otto parti: ottanti. Sono convenzionalmente numerati con numeri romani (Fig. 7).
Il più conveniente per fissare la posizione di una figura geometrica nello spazio e identificarne la forma dalle proiezioni ortogonali è il sistema di coordinate cartesiane, costituito da tre piani di proiezione reciprocamente perpendicolari. Poiché la geometria descrittiva è progettata per trasferire i risultati della sua ricerca teorica per l'uso pratico, è consigliabile considerare la proiezione ortogonale anche in un sistema di tre piani di proiezione.
Per facilità di proiezione, tre piani reciprocamente perpendicolari vengono scelti come tre piani di proiezione (Fig. 8). Uno di questi è solitamente posizionato orizzontalmente: si chiama piano di proiezione orizzontale, l'altro è verticale, parallelo al piano del disegno, si chiama piano frontale delle proiezioni ed un terzo, perpendicolare ai due esistenti - si chiama piano del profilo delle proiezioni. Questi piani di proiezione si intersecano lungo linee chiamate assi di proiezione.
Abbiamo adottato un sistema destrorso per la disposizione dei piani di proiezione. In questo caso vengono considerate le direzioni positive degli assi: per l'asse X (intersezione dei piani di proiezione orizzontale e frontale) – a sinistra dell'origine, per l'asse sì (intersezione dei piani di proiezione orizzontale e del profilo) – verso l'osservatore dal piano di proiezione frontale, per l'asse z (intersezione dei piani frontale e di profilo delle proiezioni) – verso l'alto dal piano orizzontale delle proiezioni, le direzioni opposte degli assi sono considerate negative.
La proiezione di un punto è la base della perpendicolare tracciata dal punto sul corrispondente piano di proiezione. Proiezione orizzontale i punti sono la proiezione rettangolare di un punto su un piano di proiezione orizzontale, proiezione frontale – rispettivamente sul piano frontale delle proiezioni e profilo – sul piano del profilo delle proiezioni.
È scomodo utilizzare questa disposizione spaziale per rappresentare proiezioni ortogonali di figure geometriche a causa del suo ingombro, e anche per il fatto che su quelle individuali (orizzontali e di profilo) la forma e le dimensioni della figura proiettata sono distorte. Pertanto, invece di rappresentare una disposizione spaziale in un disegno, utilizzano un disegno complesso (diagramma di Monge) composto da tre proiezioni ortogonali interconnesse di una figura geometrica.
La trasformazione della disposizione spaziale in diagrammi viene effettuata combinando i piani di proiezione orizzontale e di profilo con il piano di proiezione frontale (Fig. 7).
Poiché i piani non hanno confini, nella posizione combinata (sul diagramma) i confini dei piani non sono mostrati, non è necessario lasciare iscrizioni che indichino la posizione dei piani di proiezione (Fig. 10).
Passando al diagramma, la chiarezza spaziale è andata persa. Il diagramma offre di più: precisione e facilità di misurazione delle immagini, con semplicità di costruzione. Tuttavia, immaginare un'immagine spaziale richiede il lavoro dell'immaginazione.
Non hai trovato quello che cercavi? Usa la ricerca:
I migliori detti: Per uno studente, la cosa più importante non è superare l'esame, ma ricordarselo in tempo. 9744 — | 7364 - oppure leggi tutto.
Disegno in proiezione (cenni di geometria descrittiva)
Metodo di proiezione
Metodo di proiezione rettangolare
Se i raggi sporgenti formano un angolo retto con il piano di proiezione, vengono chiamate tali proiezioni rettangolare.
Vengono anche chiamate proiezioni rettangolari ortogonale. La parola "ortogonale" deriva dalle parole greche "ortos" - dritto e "gonia" - angolo.
I disegni nel sistema di proiezioni rettangolari forniscono un quadro completo della forma e delle dimensioni dell'oggetto. Sono più facili da eseguire rispetto alle proiezioni assonometriche.
Cosa devi sapere per completare con successo i disegni?
Qualsiasi oggetto che abbia superfici piane è limitato da vertici, bordi e facce (Fig. 108). Pertanto, per imparare a rappresentare vari oggetti nei disegni, è necessario sapere come sono rappresentati i vertici (punti), i bordi (segmenti di linee rette) e i bordi degli oggetti (parti di un piano) nelle proiezioni rettangolari.
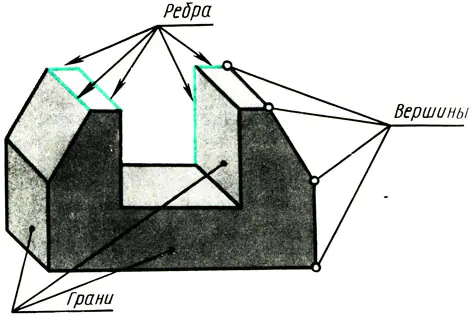
Riso. 108. Premsch come insieme di punti, scrivi. Vertici dei piani
Facciamo un semplice esperimento. Vediamo come sono raffigurati un oggetto piatto e cento elementi in diverse posizioni.
Prendiamo come piano di proiezione il muro opposto alla finestra. Lascialo fuori dalla finestra perpendicolare Raggi di luce cadono sul muro - proiettano raggi. Posizionare un foglio di carta spessa ABCD davanti al muro (parallelo ad esso) (Fig. 109, a). Sulla parete si forma un'ombra, equivalente alla proiezione dell'oggetto. Quali sono le sue dimensioni? In questo caso la proiezione a’b’c’d’ corrisponde per forma e dimensione all’oggetto della proiezione: il foglio
ABCD. Il metodo di proiezione è rettangolare, poiché i raggi proiettanti sono perpendicolari al piano di proiezione.
Come cambierà la proiezione se l'oggetto raffigurato viene ruotato, ad esempio, attorno alla sua altezza - bordo AD (Fig. 109, b)?
Quando si gira, l'ombra si ridurrà in larghezza (le linee a'b' e c'd' nella Fig. 109, b si accorciano). Continuando a ruotare il foglio di carta, notiamo che in posizione perpendicolare al muro, l'immagine del foglio si trasformerà in una linea (Fig. 109, c), ma l'altezza dell'oggetto rimane costante, cioè linee a' d' e b'c' lungo la lunghezza non sono distorti.
Ora formuliamo conclusioni su quale forma e dimensione ha l'immagine di un oggetto piatto in proiezioni rettangolari, posizionate diversamente rispetto al piano di proiezione:
a) su di esso è raffigurata una figura piatta parallela al piano di proiezione a grandezza naturale (Fig. 109, a);
b) su di essa è raffigurata una figura piatta, inclinata rispetto al piano di proiezione con una distorsione delle dimensioni (Fig. 109, b);
c) su di essa è raffigurata una figura piatta perpendicolare al piano di proiezione sotto forma di un segmento di linea retta (Fig. 109, c).
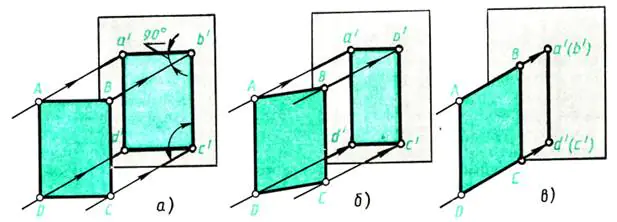
Riso. 109. Proiezione di una figura piatta
Questi risultati riguardano la rappresentazione dei bordi degli oggetti.
Come vengono rappresentati i bordi degli oggetti, cioè le linee, nelle proiezioni rettangolari?
Ripetiamo l'esperimento ruotando un oggetto piatto, osserviamo come vengono proiettati i suoi bordi, cioè le linee, e traiamo le conclusioni:
a) su di esso è raffigurato un segmento di linea retta parallelo al piano di proiezione a grandezza naturale (confronta l'altezza dell'oggetto AD e BC in Fig. 109, a, b, c con le sue proiezioni a'd' e b'c, e la larghezza dell'oggetto AB e CD con le sue sporgenze a'b' e c'd' nella fig. 109, a);
b) su di esso è raffigurato un segmento diritto inclinato rispetto al piano di proiezione con una distorsione in lunghezza (confrontare la larghezza dell'oggetto AB e CD in Fig. 109, b con le sue proiezioni a'b' e c'd');
c) un segmento di linea retta perpendicolare al piano di proiezione è rappresentato da un punto su di esso (vedere in Fig. 109, attraverso la larghezza dell'oggetto - linee AB e CD, perpendicolari al piano di proiezione).
La proiezione di un punto è la base di una perpendicolare abbassata da un dato punto dello spazio sul piano di proiezione (vedi punti a', b', c', d' - proiezioni dei punti A, B, C, D).
Accettiamo di denotare i punti nello spazio con le lettere maiuscole A, B, C, D, ecc., e le proiezioni dei punti con le corrispondenti lettere minuscole i, b, c, d, ecc.
Dei due punti coincidenti nel disegno (Fig. 109, c), uno è l'immagine di un vertice visibile e l'altro è invisibile (chiuso). La designazione delle proiezioni dei vertici invisibili è riportata tra parentesi.



