Osat: Tekniikka
Oppitunnin tavoitteet ja tavoitteet:
koulutuksellinen: näytä opiskelijoille, kuinka käyttää suorakaiteen projektiomenetelmää piirustuksen tekemisessä;
• tarve käyttää kolmea projektiotasoa;
• luoda edellytykset taitojen muodostumiselle objektin projisoimiseksi kolmelle projektiotasolle;
kehitetään: kehittää tilakäsitteitä, tilaajattelua, kognitiivista kiinnostusta ja opiskelijoiden luovia kykyjä;
kouluttaa: vastuullinen asenne piirtämiseen, graafisen työn kulttuurin kehittäminen.
Opetusmenetelmät ja -tekniikat: selitys, keskustelu, ongelmatilanteet, tutkimus, harjoitukset, frontaalityöskentely luokan kanssa, luova työskentely.
Materiaalituki: tietokoneet, esitys "Suorakulmaprojektio", tehtävät, harjoitukset, harjoituskortit, esitys itsetestaukseen.
Oppitunnin tyyppi: oppitunti tiedon lujittamiseksi.
Sanastotyö: vaakataso, projektio, projektio, profiili, tutkimus, projekti.
I. Organisatorinen osa.
Kerro oppitunnin aihe ja tarkoitus.
Toteutetaan oppitunti-kilpailu, jokaisesta tehtävästä saat tietyn määrän pisteitä. Saaduista pisteistä riippuen oppitunnille annetaan arvosana.
II. Projektion toisto ja sen tyypit.
Projektio on henkinen prosessi, jossa luodaan kuvia kohteista tasossa.
Toisto suoritetaan esityksen avulla.
1. Opiskelijoilta kysytään ongelmallinen tilanne. (Esitys 1)
Analysoi etuprojektion osan geometrinen muoto ja löydä tämä osa visuaalisten kuvien joukosta.

Tästä tilanteesta päätellään, että kaikilla 6 osalla on sama etuuloke. Tämä tarkoittaa, että yksi projektio ei aina anna täydellistä kuvaa osan muodosta ja suunnittelusta.
- Mikä on tie ulos tästä tilanteesta? (Katso osaa toiselta puolelta).
2. Oli tarpeen käyttää toista projektiotasoa. (Vaakasuuntainen projektio).
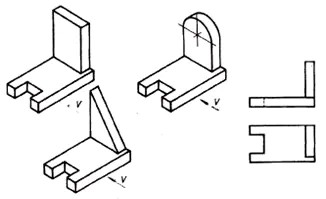
3. Kolmannen projektion tarve syntyy, kun kaksi projektiota ei riitä määrittämään kohteen muotoa.
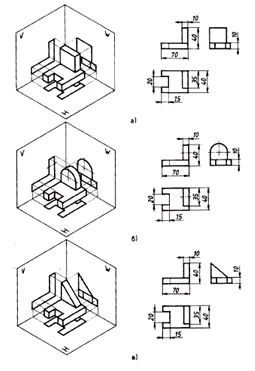
Mitoitus:
- etuprojektiossa -
Johtopäätös: tämä tarkoittaa, että oppiaksesi tekemään piirustuksia sinun on kyettävä projisoimaan esineitä tasolle.
Täydennä määritelmätekstin puuttuvat sanat.
1. On olemassa _______________ ja __________________ projektio.
2. Jos yhdestä pisteestä tulee ______________ säteitä, projektiota kutsutaan ______________.
3. Jos ______________ säteet on suunnattu rinnakkain, projektiota kutsutaan _____________.
4. Jos ______________ säteitä on suunnattu yhdensuuntaisesti toistensa kanssa ja 90° kulmassa projektiotasoon nähden, niin projektiota kutsutaan __________________.
5. Luonnollinen kuva esineestä projektiotasolla saadaan vain __________________ projektiolla.
6. Ulokkeet sijaitsevat suhteessa toisiinsa___________________________________.
7. Suorakaiteen projektiomenetelmän perustaja on _______________
Tehtävä 2. Tutkimusprojekti
Yhdistä numeroilla merkityt päätyypit kirjaimilla merkittyihin osiin ja kirjoita vastaus vihkoon.
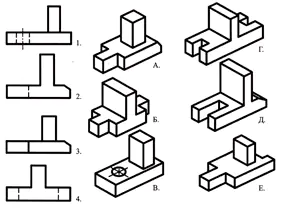
Harjoitus geometristen kappaleiden tuntemuksen tarkistamiseksi.
Etsi osasta visuaalinen kuva sanallisen kuvauksen avulla.
Kappaleen pohja on suorakaiteen muotoisen suuntaissärmiön muotoinen, jonka pienemmillä pinnoilla on säännöllisen nelikulmaisen prisman muotoisia uria. Suuntaissärmiön yläpinnan keskellä on katkaistu kartio, jonka akselia pitkin on läpimenevä sylinterimäinen reikä.
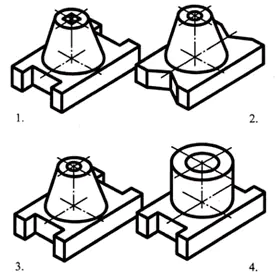
Vastaus: osa nro 3 (1 piste)
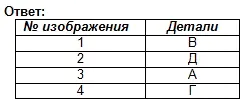
Etsi osien teknisten piirustusten ja niiden etuulokkeiden välinen vastaavuus (projektiosuunta on merkitty nuolella). Piirrä hajallaan olevien kuvien perusteella jokaisesta osasta piirros, joka koostuu kolmesta kuvasta. Kirjoita vastauksesi taulukkoon (Kuva 129).
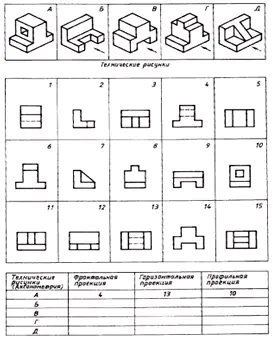
| Tekniset piirustukset | Etuprojektio | Vaakasuora projektio | Profiilin projektio |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| SISÄÄN | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Käytännön työ.
Tehtävä nro 1. Tutkimusprojekti
Etsi tämän visuaalisen kuvan etu- ja vaakaprojektio. Kirjoita vastaus muistikirjaasi.
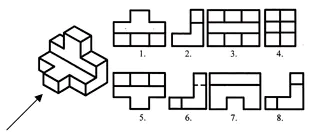
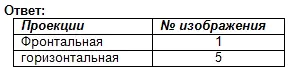
Työn arviointi oppitunnilla. Itsetestaus. (Esitys 2)
Työn ensimmäisen osan pisteet kirjoitetaan taululle:
Tehtävä nro 2. Luova työ ja sen toteutumisen todentaminen
(luova projekti)
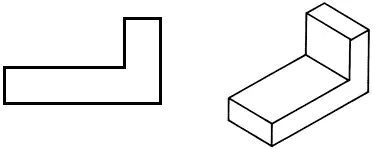
• Piirrä edestä projektio työkirjaasi.
• Piirrä vaakasuora projektio muuttaen kappaleen muotoa sen massan pienentämiseksi.
• Tee tarvittaessa muutoksia frontaaliseen projektioon.
• Tarkista tehtävän suorittaminen kutsumalla yksi tai kaksi oppilasta taululle selittämään heidän ratkaisunsa ongelmaan.
IV. Yhteenveto oppitunnista.
1. Työn arviointi oppitunnilla. (Työn käytännön osan tarkistaminen)
V. Kotitehtävä.
1. Tutkimusprojekti.
Työskentele taulukon mukaan: määritä, mikä numerolla merkitty piirros vastaa kirjaimella merkittyä piirustusta.
Rinnakkaisprojektion erikoistapaus, jossa projektion suunta on kohtisuorassa projektiotasoon nähden, on ns. suorakulmainen tai ortogonaalinen projektio. Pisteen suorakulmainen (ortogonaalinen) projektio on pisteestä projektiotasoon vedetyn kohtisuoran kanta. Pisteiden A ja B suorakulmainen projektio on esitetty kuvassa. 5.
Pisteen sijainnin määrittämiseksi avaruudessa sen yhdensuuntaisista projektioista tarvitaan kaksi yhdensuuntaista tasoa, jotka on saatu kahteen projektion suuntaan.
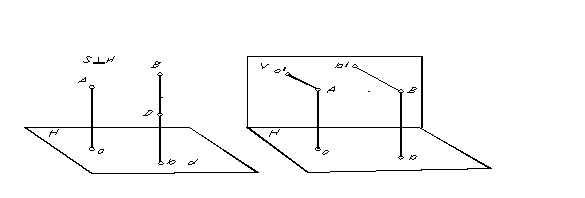 |
Koska pisteen läpi voidaan vetää vain yksi tasoon nähden kohtisuora suora, niin tietysti ortogonaalisella projektiolla, jotta saadaan kaksi projektiota yhdestä pisteestä, tarvitaan kaksi ei-rinnakkaista projektiotasoa (kuva 6) .
Ortografisella projektiolla on useita etuja keski- ja rinnakkaisprojektioon verrattuna. Näitä ovat ensisijaisesti:
1. Graafisten rakenteiden yksinkertaisuus pisteiden ortogonaalisten projektioiden määrittämiseksi.
2. Kyky tietyissä olosuhteissa säilyttää projisoidun hahmon muoto ja koko projektioissa.
Todetut edut ovat varmistaneet ortogonaalisen projektion laajan käytön tekniikassa, erityisesti koneenrakennuspiirustusten laadinnassa.
Konetekniikassa, jotta piirustuksen perusteella voitaisiin arvioida kuvattujen esineiden muotoa ja kokoa, piirustuksia tehdessään he eivät yleensä käytä kahta, vaan useita projektiotasoja.
Pisteen sijainti avaruudessa ja siten minkä tahansa geometrisen kuvion sijainti voidaan määrittää, jos jokin koordinaattiviittausjärjestelmä on määritetty. Projektiotasot jakavat tilan kahdeksaan osaan - oktanttiin. Ne on perinteisesti numeroitu roomalaisilla numeroilla (kuva 7).
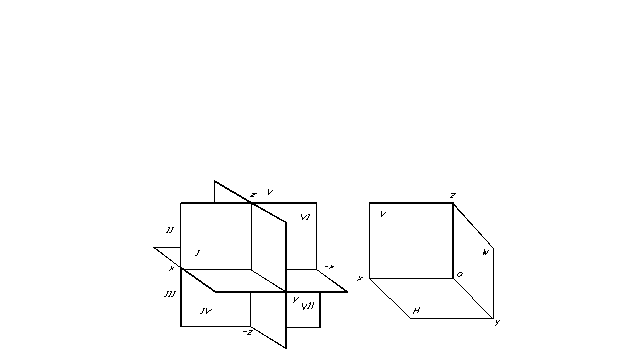
Projektiotasot jakavat tilan kahdeksaan osaan - oktanttiin. Ne on perinteisesti numeroitu roomalaisilla numeroilla (kuva 7).
Kätevin geometrisen kuvion paikan kiinnittämiseen avaruudessa ja sen muodon tunnistamiseen kohtisuorasta projektiosta on karteesinen koordinaattijärjestelmä, joka koostuu kolmesta keskenään kohtisuorassa olevasta projektiotasosta. Koska kuvaava geometria on suunniteltu välittämään teoreettisen tutkimuksensa tuloksia käytännön käyttöön, on suositeltavaa tarkastella ortogonaalista projektiota myös kolmen projektiotason järjestelmässä.
Projisoinnin helpottamiseksi kolmeksi projektiotasoksi valitaan kolme keskenään kohtisuoraa tasoa (kuva 8). Yksi niistä sijoitetaan yleensä vaakasuoraan - sitä kutsutaan vaakasuora projektiotaso, toinen on pystysuora, yhdensuuntainen piirustustason kanssa, sitä kutsutaan projektioiden etutaso ja kolmas, kohtisuorassa kahteen olemassa olevaan - sitä kutsutaan projektioiden profiilitaso. Nämä projektiotasot leikkaavat ns projektioakselit.
Olemme ottaneet käyttöön oikeakätisen järjestelmän projektiotasojen järjestämiseen. Tässä tapauksessa huomioidaan akselien positiiviset suunnat: akselille X (vaaka- ja etuprojektiotasojen leikkauspiste) – akselin origon vasemmalla puolella y (vaaka- ja profiiliprojektiotasojen leikkauspiste) – kohti tarkkailijaa etuprojektiotasosta, akselille z (projektioiden etu- ja profiilitason leikkauspiste) – projektioiden vaakatasosta ylöspäin akselien vastakkaiset suunnat katsotaan negatiivisiksi.
Pisteen projektio on pisteestä vastaavalle projektiotasolle vedetyn kohtisuoran kanta. Vaakasuora projektio pisteet ovat pisteen suorakulmainen projektio vaakasuoralla projektiotasolla, edestä projektio – projektioiden etutasolla ja vastaavasti profiili - projektioiden profiilitasolla.
On hankalaa käyttää tätä spatiaalista asettelua geometristen kuvioiden kohtisuorien projektioiden kuvaamiseen sen tilavuuden vuoksi ja myös sen vuoksi, että yksittäisissä kuvissa (vaaka ja profiili) projisoidun hahmon muoto ja koko ovat vääristyneet. Siksi sen sijaan, että ne esittäisivät tila-asetelman piirustuksessa, he käyttävät monimutkaista piirustusta (Monge-kaavio), joka koostuu kolmesta toisiinsa yhdistetystä geometrisen hahmon ortogonaalisesta projektiosta.
Tila-asetelman muuntaminen kaavioiksi suoritetaan yhdistämällä vaaka- ja profiiliprojektiotaso etuprojektiotasoon (kuva 7).
Koska tasoilla ei ole rajoja, yhdistetyssä asennossa (kaaviossa) tasojen rajoja ei näytetä, joten projektiotasojen sijaintia osoittavia merkintöjä ei tarvitse jättää (kuva 10).
Kaavioon siirtymisen jälkeen avaruudellinen selkeys katosi. Kaavio antaa enemmän - tarkkuutta ja kuvien mittaamisen helppoutta rakentamisen yksinkertaisuudella. Tilakuvan kuvitteleminen vaatii kuitenkin mielikuvituksen työtä.
Etkö löytänyt etsimääsi? Käytä hakua:
Parhaat sanat: Opiskelijalle tärkeintä ei ole kokeen läpäiseminen, vaan sen muistaminen ajoissa. 9744 — | 7364 - tai lue kaikki.
Projektiopiirustus (kuvausgeometrian perusteet)
Projektiomenetelmä
Suorakaiteen projektiomenetelmä
Jos ulkonevat säteet muodostavat suoran kulman projektiotasoon, niin tällaisia projektioita kutsutaan suorakulmainen.
Suorakulmaisia projektioita kutsutaan myös ortogonaalinen. Sana "ortogonaalinen" tulee kreikan sanoista "ortos" - suora ja "gonia" - kulma.
Suorakaiteen muotoisten projektioiden järjestelmän piirustukset antavat täydellisen kuvan kohteen muodosta ja koosta. Ne on helpompi suorittaa kuin aksonometriset projektiot.
Mitä sinun tulee tietää, jotta voit suorittaa piirustukset onnistuneesti?
Kaikki esineet, joilla on tasaiset pinnat, on rajoitettu kärkipisteillä, reunoilla ja pinnoilla (kuva 108). Siksi, jotta voit oppia kuvaamaan erilaisia objekteja piirustuksissa, sinun on tiedettävä, kuinka kohteiden kärjet (pisteet), reunat (suorien viivojen segmentit) ja objektien reunat (tason osat) on kuvattu suorakaiteen muotoisissa projektioissa.
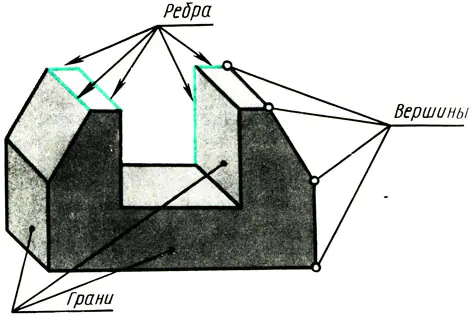
Riisi. 108. Premsch pistejoukona, kirjoita. Tasojen huiput
Tehdään yksinkertainen kokeilu. Katsotaan kuinka litteä esine ja sata elementtiä on kuvattu eri asennoissa.
Otetaan ikkunaa vastapäätä oleva seinä projektiotasoksi. Anna sen ulos ikkunasta kohtisuorassa Valosäteet putoavat seinälle - ulkonevia säteitä. Aseta paksu ABCD-paperiarkki seinän eteen (sen suuntaisesti) (kuva 109, a). Seinään muodostuu varjo, joka vastaa kohteen projektiota. Mitkä ovat sen mitat? Tässä tapauksessa projektio a’b’c’d’ vastaa muodoltaan ja kooltaan projektiokohdetta - arkkia
ABCD. Projektiomenetelmä on suorakaiteen muotoinen, koska projisoidut säteet ovat kohtisuorassa projektiotasoon nähden.
Miten projektio muuttuu, jos kuvattua kohdetta käännetään esimerkiksi korkeutensa ympäri - reuna AD (kuva 109, b)?
Käännettäessä varjo kutistuu leveydeltään (viivat a’b’ ja c’d’ kuvassa 109, b lyhenevät). Jatkamalla paperiarkin pyörittämistä huomaamme, että seinään nähden kohtisuorassa asennossa arkin kuva muuttuu viivaksi (kuva 109, c), mutta kohteen korkeus pysyy vakiona, eli viivat a' d' ja b'c' eivät ole vääristyneet.
Tehdään nyt johtopäätökset siitä, minkä muotoisia ja kokoisia kuvia litteällä esineellä on suorakaiteen muotoisissa projektioissa, jotka sijaitsevat eri tavalla suhteessa projektiotasoon:
a) siihen on esitetty projektiotason suuntainen litteä hahmo luonnollisessa koossa (kuva 109, a);
b) litteä hahmo, joka on kallistettu projektiotasoon nähden, on kuvattu siinä mittojen vääristymänä (kuva 109, b);
c) siihen on kuvattu suoraviivaisen segmentin muodossa litteä, kohtisuorassa projektiotasoon nähden (kuva 109, c).
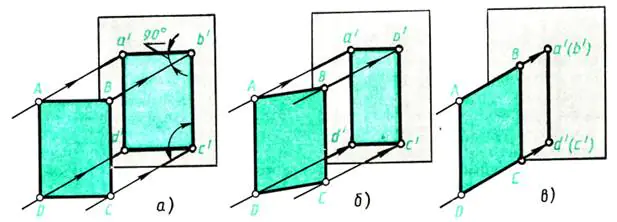
Riisi. 109. Litteän hahmon projisointi
Nämä havainnot liittyvät esineiden reunojen kuvaamiseen.
Miten objektien reunat eli viivat on kuvattu suorakaiteen muotoisissa projektioissa?
Toistetaan koe litteän esineen pyörittämisellä, tarkkaillaan kuinka sen reunat eli viivat projisoidaan ja tehdään johtopäätökset:
a) sille on esitetty projektiotason suuntainen suorasegmentti luonnollisessa koossa (vertaa kohteen AD ja BC korkeutta kuvassa 109, a, b, c projektioineen a'd' ja b'c, ja objektin AB ja CD leveys projektioineen a'b' ja c'd' kuviossa 109, a);
b) siinä on kuvattu suora segmentti, joka on vinossa projektiotasoon nähden pituudeltaan vääristyneenä (vertaa kohteen AB ja CD leveyttä kuvassa 109, b sen projektioineen a’b’ ja c’d’);
c) projektiotasoon nähden kohtisuorassa oleva suora jana on kuvattu sen päällä olevalla pisteellä (katso kuva 109, objektin leveyden poikki - suorat AB ja CD, kohtisuorassa projektiotasoon nähden).
Pisteen projektio on tietystä avaruuden pisteestä projektiotasolle lasketun kohtisuoran kanta (katso pisteet a’, b’, c’, d’ - pisteiden A, B, C, D projektiot).
Sovitaan, että avaruuden pisteet merkitään isoilla kirjaimilla A, B, C, D jne. ja pisteiden projektiot vastaavilla pienillä kirjaimilla i, b, c, d jne.
Piirustuksen kahdesta samasta pisteestä (kuva 109, c) toinen on kuva näkyvästä kärjestä ja toinen on näkymätön (suljettu). Näkymättömien kärkien projektioiden nimitys on otettu suluissa.



