Seksjoner: Teknologi
Mål og mål for leksjonen:
pedagogisk: vise elevene hvordan de bruker den rektangulære projeksjonsmetoden når de lager en tegning;
• behovet for å bruke tre projeksjonsplaner;
• skape forhold for dannelse av ferdigheter for å projisere et objekt på tre projeksjonsplaner;
utvikle: utvikle romlige konsepter, romlig tenkning, kognitiv interesse og kreative evner til elever;
utdanne: ansvarlig holdning til tegning, å dyrke en kultur for grafisk arbeid.
Metoder og teknikker for undervisning: forklaring, samtale, problemsituasjoner, forskning, øvelser, frontalarbeid med klassen, kreativt arbeid.
Materialstøtte: datamaskiner, presentasjon "Rektangulær projeksjon", oppgaver, øvelser, øvingskort, presentasjon for selvtest.
Leksjonstype: leksjon for å konsolidere kunnskap.
Ordforrådsarbeid: horisontalplan, projeksjon, projeksjon, profil, forskning, prosjekt.
I. Organisasjonsdel.
Oppgi tema og formål med leksjonen.
La oss gjennomføre leksjon-konkurranse, for hver oppgave vil du motta et visst antall poeng. Avhengig av poengsummen vil en karakter for timen bli tildelt.
II. Repetisjon av projeksjon og dens typer.
Projeksjon er den mentale prosessen med å konstruere bilder av objekter på et plan.
Repetisjon utføres ved hjelp av presentasjon.
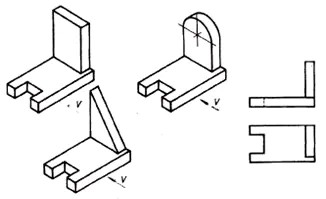
1. Elevene blir spurt problematisk situasjon. (Presentasjon 1)
Analyser den geometriske formen til delen på frontprojeksjonen og finn denne delen blant de visuelle bildene.

Fra denne situasjonen konkluderes det med at alle 6 delene har samme frontalprojeksjon. Dette gjør at én projeksjon ikke alltid gir et fullstendig bilde av delens form og utforming.
– Hva er veien ut av denne situasjonen? (Se på delen fra den andre siden).
2. Det var behov for å bruke et annet projeksjonsplan. (Horisontal projeksjon).
3. Behovet for en tredje projeksjon oppstår når to projeksjoner ikke er nok til å bestemme formen til et objekt.
Størrelse:
- på frontalprojeksjonen –
Konklusjon: dette betyr at for å lære å lage tegninger, må du kunne projisere objekter på et fly.
Fyll inn de manglende ordene i definisjonsteksten.
1. Det er _______________ og ______________ projeksjon.
2. Hvis ______________ stråler kommer ut fra ett punkt, kalles projeksjon ______________.
3. Hvis ______________ stråler er rettet parallelt, kalles projeksjon _____________.
4. Hvis ______________ stråler er rettet parallelt med hverandre og i en vinkel på 90 ° til projeksjonsplanet, kalles projeksjonen ______________.
5. Et naturlig bilde av et objekt på et projeksjonsplan oppnås kun med ______________ projeksjon.
6. Fremspringene er plassert i forhold til hverandre______________________________.
7. Grunnleggeren av den rektangulære projeksjonsmetoden er _______________
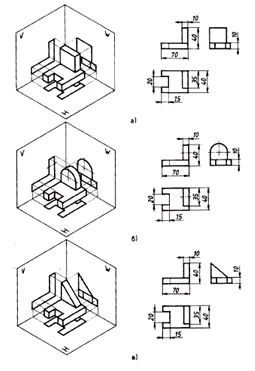
Oppgave 2. Forskningsprosjekt
Match hovedtypene angitt med tall med delene angitt med bokstaver, og skriv svaret i notatboken.
En øvelse for å gjennomgå kunnskap om geometriske legemer.
Bruk den verbale beskrivelsen til å finne et visuelt bilde av delen.
Basen av delen har formen av et rektangulært parallellepiped, hvis mindre flater har spor i form av et vanlig firkantet prisme. I midten av oversiden av parallellepipedet er det en avkortet kjegle, langs aksen som det er et gjennomgående sylindrisk hull.
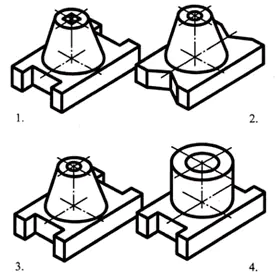
Svar: del nr. 3 (1 poeng)
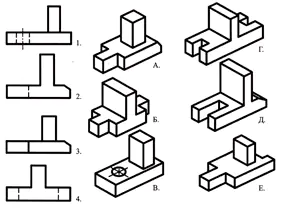
Finn samsvaret mellom de tekniske tegningene av delene og deres frontale fremspring (projeksjonsretningen er markert med en pil). Basert på de spredte bildene av tegningen, lag en tegning av hver del, bestående av tre bilder. Skriv svaret ditt i tabellen (fig. 129).
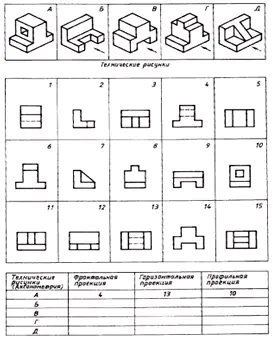
| Tekniske tegninger | Frontal projeksjon | Horisontal projeksjon | Profilprojeksjon |
| EN | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| I | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktisk jobb.
Oppgave nr. 1. Forskningsprosjekt
Finn frontale og horisontale projeksjoner for dette visuelle bildet. Skriv svaret i notatboka.
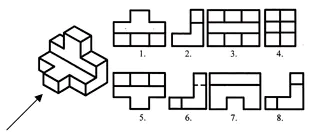
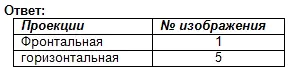
Vurdering av arbeid i timen. Selv test. (Presentasjon 2)
Poengene for karaktersetting av første del av arbeidet er skrevet på tavlen:
Oppgave nr. 2. Kreativt arbeid og verifisering av implementeringen
(kreativt prosjekt)
• Tegn frontprojeksjonen inn i arbeidsboken din.
• Tegn en horisontal projeksjon, endre formen på delen for å redusere massen.
• Gjør om nødvendig endringer i frontprojeksjonen.
• For å kontrollere at oppgaven er fullført, kall en eller to elever til styret for å forklare deres løsning på problemet.
IV. Oppsummering av leksjonen.
1. Vurdering av arbeid i timen. (Sjekker den praktiske delen av arbeidet)
V. Lekseoppgave.
1. Forskningsprosjekt.
Arbeid i henhold til tabellen: bestem hvilken tegning, utpekt med et tall, som tilsvarer tegningen, utpekt med en bokstav.
Et spesielt tilfelle av parallell projeksjon, der projeksjonsretningen er vinkelrett på projeksjonsplanet, kalles rektangulær eller ortogonal projeksjon. Den rektangulære (ortogonale) projeksjonen av et punkt er bunnen av vinkelrett tegnet fra punktet til projeksjonsplanet. Den rektangulære projeksjonen av punktene A og B er vist i fig. 5.
For å bestemme posisjonen til et punkt i rommet fra dets parallelle projeksjoner, er det nødvendig å ha to parallelle plan oppnådd i to projeksjonsretninger.
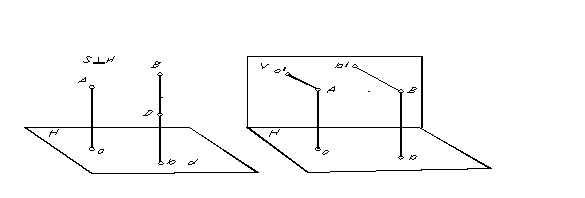 |
Fordi gjennom et punkt kan bare én rett linje vinkelrett på planet tegnes, så med ortogonal projeksjon, for å få to projeksjoner av ett punkt, er det selvsagt nødvendig å ha to ikke-parallelle projeksjonsplan (fig. 6) .
Ortografisk projeksjon har en rekke fordeler fremfor sentral og parallell projeksjon. Disse inkluderer først og fremst:
1. Enkelhet av grafiske konstruksjoner for å bestemme ortogonale projeksjoner av punkter.
2. Evnen til, under visse forhold, å bevare formen og størrelsen til den projiserte figuren på fremspring.
De bemerkede fordelene har sikret utbredt bruk av ortogonal projeksjon i teknologi, spesielt for utarbeidelse av maskintekniske tegninger.
I maskinteknikk, for å kunne bedømme formen og størrelsen på gjenstandene som er avbildet fra en tegning, bruker de som regel ikke to, men flere projeksjonsplaner når de tegner tegninger.
Posisjonen til et punkt i rommet, og derfor til enhver geometrisk figur, kan bestemmes hvis et hvilket som helst koordinatreferansesystem er spesifisert. Projeksjonsplan deler rommet i åtte deler - oktanter. De er konvensjonelt nummerert med romertall (fig. 7).
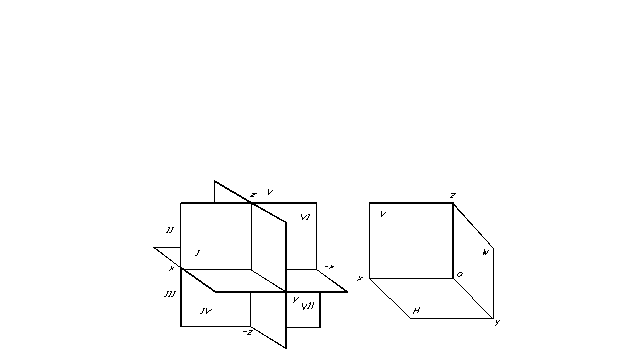
Projeksjonsplan deler rommet i åtte deler - oktanter. De er konvensjonelt nummerert med romertall (fig. 7).
Det mest praktiske for å fikse posisjonen til en geometrisk figur i rommet og identifisere dens form fra ortogonale projeksjoner er det kartesiske koordinatsystemet, som består av tre gjensidig vinkelrette projeksjonsplaner. På grunn av det faktum at beskrivende geometri er designet for å formidle resultatene av sin teoretiske forskning for praktisk bruk, er det tilrådelig å vurdere ortogonal projeksjon også i et system med tre projeksjonsplan.
For enkel projeksjon velges tre innbyrdes perpendikulære plan som tre projeksjonsplan (fig. 8). En av dem er vanligvis plassert horisontalt - det kalles horisontalt projeksjonsplan, den andre er vertikal, parallelt med tegneplanet, kalles det frontalplan av projeksjoner og en tredje, vinkelrett på de to eksisterende - heter det profilplan for projeksjoner. Disse projeksjonsplanene skjærer hverandre langs linjer kalt projeksjonsakser.
Vi har tatt i bruk et høyrehendt system for å arrangere projeksjonsplan. I dette tilfellet vurderes de positive retningene til aksene: for aksen X (skjæringspunktet mellom horisontale og frontale projeksjonsplaner) – til venstre for origo, for aksen y (skjæringspunktet mellom horisontal- og profilprojeksjonsplan) – mot observatøren fra frontprojeksjonsplanet, for aksen z (skjæringspunktet mellom front- og profilplanene til projeksjoner) - oppover fra det horisontale planet av projeksjoner, anses de motsatte retningene til aksene som negative.
Projeksjonen av et punkt er bunnen av perpendikulæren trukket fra punktet til det tilsvarende projeksjonsplanet. Horisontal projeksjon punkter er den rektangulære projeksjonen av et punkt på et horisontalt projeksjonsplan, frontal projeksjon – henholdsvis på frontalplanet av projeksjoner og profil – på profilplanet til projeksjoner.
Det er upraktisk å bruke denne romlige utformingen til å skildre ortogonale projeksjoner av geometriske figurer på grunn av dens omfang, og også på grunn av det faktum at på individuelle (horisontale og profiler) formen og størrelsen på den projiserte figuren er forvrengt. Derfor, i stedet for å skildre en romlig layout i en tegning, bruker de en kompleks tegning (Monge-diagram) som er sammensatt av tre sammenkoblede ortogonale projeksjoner av en geometrisk figur.
Transformasjonen av det romlige oppsettet til diagrammer utføres ved å kombinere horisontal- og profilprojeksjonsplanene med frontprojeksjonsplanet (fig. 7).
Siden planene ikke har noen grenser, i den kombinerte posisjonen (på diagrammet) er grensene til planene ikke vist, er det ikke nødvendig å legge igjen inskripsjoner som indikerer posisjonen til projeksjonsplanene (fig. 10).
Etter å ha byttet til diagrammet, gikk romlig klarhet tapt. Diagrammet gir mer - nøyaktighet og enkel måling av bilder, med enkel konstruksjon. For å forestille seg et romlig bilde krever imidlertid fantasiarbeid.
Fant du ikke det du lette etter? Bruk søket:
Beste ordtak: For en student er det viktigste ikke å bestå eksamen, men å huske på det i tide. 9744 — | 7364 - eller les alt.
Projeksjonstegning (grunnleggende om beskrivende geometri)
Projeksjonsmetode
Rektangulær projeksjonsmetode
Hvis de utstikkende strålene danner en rett vinkel med projeksjonsplanet, kalles slike projeksjoner rektangulær.
Rektangulære projeksjoner kalles også ortogonal. Ordet "ortogonal" kommer fra de greske ordene "ortos" - rett og "gonia" - vinkel.
Tegninger i systemet med rektangulære projeksjoner gir et komplett bilde av formen og størrelsen på objektet. De er lettere å utføre enn aksonometriske projeksjoner.
Hva trenger du å vite for å fullføre tegninger?
Enhver gjenstand som har flate overflater er begrenset av hjørner, kanter og flater (fig. 108). Derfor, for å lære å avbilde ulike objekter i tegninger, må du vite hvordan hjørner (punkter), kanter (segmenter av rette linjer) og kanter av objekter (deler av et plan) er avbildet i rektangulære projeksjoner.
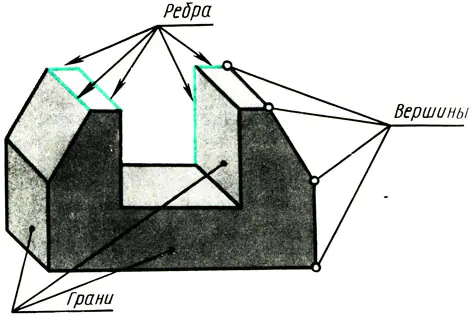
Ris. 108. Premsch som et sett med punkter, skriv. Topppunkter av fly
La oss gjøre et enkelt eksperiment. La oss se hvordan en flat gjenstand og hundre elementer er avbildet i forskjellige posisjoner.
La oss ta veggen overfor vinduet som projeksjonsplan. Slipp den ut av vinduet vinkelrett Stråler av lys faller på veggen - utstrålende stråler. Plasser et ark med tykt ABCD-papir foran veggen (parallelt med den) (fig. 109, a). Det dannes en skygge på veggen, tilsvarende projeksjonen av objektet. Hva er dens dimensjoner? I dette tilfellet tilsvarer projeksjonen a'b'c'd' i form og størrelse objektet for projeksjonen - arket
ABCD. Projeksjonsmetoden er rektangulær, siden de projiserte strålene er vinkelrett på projeksjonsplanet.
Hvordan vil projeksjonen endres hvis det avbildede objektet roteres, for eksempel rundt høyden - kanten AD (fig. 109, b)?
Ved vending vil skyggen krympe i bredden (linjene a’b’ og c’d’ i fig. 109, b blir kortere). Fortsetter vi å rotere papirarket, legger vi merke til at i en posisjon vinkelrett på veggen, vil bildet av arket bli til en linje (fig. 109, c), men høyden på objektet forblir konstant, dvs. linjene a' d' og b'c' langs lengden er ikke forvrengt.
La oss nå formulere konklusjoner om hvilken form og størrelse bilder et flatt objekt har i rektangulære projeksjoner, annerledes plassert i forhold til projeksjonsplanet:
a) en flat figur parallelt med projeksjonsplanet er avbildet på den i naturlig størrelse (fig. 109, a);
b) en flat figur, skråstilt til projeksjonsplanet, er avbildet på den med en forvrengning av dimensjoner (fig. 109, b);
c) en flat figur vinkelrett på projeksjonsplanet er avbildet på den i form av et rett linjesegment (fig. 109, c).
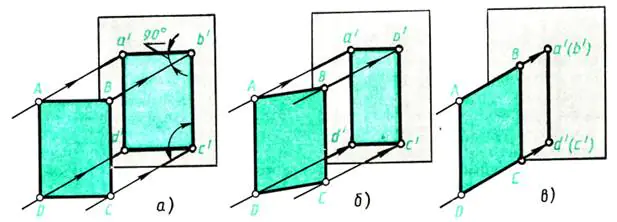
Ris. 109. Projisere en flat figur
Disse funnene relaterer seg til avbildningen av kantene på objekter.
Hvordan er kantene på objekter, det vil si linjer, avbildet i rektangulære projeksjoner?
La oss gjenta eksperimentet med å rotere en flat gjenstand, observere hvordan kantene, dvs. linjene, projiseres, og trekke konklusjoner:
a) et rett linjesegment parallelt med projeksjonsplanet er avbildet på det i naturlig størrelse (sammenlign høyden til objektet AD og BC i fig. 109, a, b, c med projeksjonene a'd' og b'c, og bredden av objektet AB og CD med dets fremspring a'b' og c'd' i fig. 109, a);
b) et rett segment skrått mot projeksjonsplanet er avbildet på det med en forvrengning i lengden (sammenlign bredden til objektet AB og CD i fig. 109, b med dets projeksjoner a'b' og c'd');
c) et rett linjesegment vinkelrett på projeksjonsplanet er avbildet av et punkt på det (se i fig. 109, på tvers av objektets bredde - linjene AB og CD, vinkelrett på projeksjonsplanet).
Projeksjonen av et punkt er bunnen av en perpendikulær senket fra et gitt punkt i rommet til projeksjonsplanet (se punktene a’, b’, c’, d’ - projeksjoner av punktene A, B, C, D).
La oss bli enige om å betegne punkter i rommet med store bokstaver A, B, C, D, etc., og projeksjoner av punkter med de tilsvarende små bokstavene i, b, c, d, etc.
Av de to punktene som faller sammen på tegningen (fig. 109, c), er det ene et bilde av et synlig toppunkt, og det andre er et usynlig (lukket) et. Betegnelsen på projeksjoner av usynlige hjørner er tatt i parentes.



