セクション: テクノロジー
レッスンの目標と目的:
教育的: 図面を作成するときに長方形の投影法を使用する方法を生徒に示します。
• 3 つの投影面を使用する必要がある。
• オブジェクトを 3 つの投影面に投影するスキルを形成するための条件を作成します。
現像: 学生の空間概念、空間的思考、認知的興味、創造的能力を開発します。
教育: 描画に対する責任ある態度を身に付け、グラフィックワークの文化を育みます。
指導方法と技術: 説明、会話、問題状況、調査、演習、クラスでの正面からの取り組み、創造的な作業。
教材サポート: コンピューター、プレゼンテーション「長方形投影法」、タスク、演習、演習カード、自己テスト用のプレゼンテーション。
レッスンの種類: 知識を定着させるためのレッスン。
語彙作業: 水平面、投影、投影、プロファイル、研究、プロジェクト。
I. 組織的な部分。
レッスンのテーマと目的を述べます。
実行しましょう レッスン・コンテスト, タスクごとに一定のポイントを獲得できます。得点に応じて、レッスンのグレードが割り当てられます。
II.投影の繰り返しとその種類。
投影は、オブジェクトのイメージを平面上に構築する精神的なプロセスです。
繰り返しはプレゼンテーションを使用して実行されます。
1. 生徒たちに聞かれるのは 問題のある状況。 (プレゼンテーション1)
正面投影上の部品の幾何学的形状を分析し、視覚画像の中からその部品を見つけます。

この状況から、6 つのパーツすべての正面投影が同じであると結論付けられます。これは、1 つの投影からは部品の形状と設計の完全な全体像が常に得られるわけではないことを意味します。
- この状況から抜け出す方法は何ですか? (その部分を反対側から見てください。)
2. 別の投影面を使用する必要がありました。 (水平投影)。
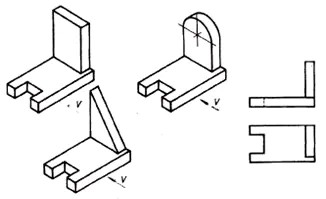
3. オブジェクトの形状を決定するのに 2 つの投影では不十分な場合、3 番目の投影が必要になります。
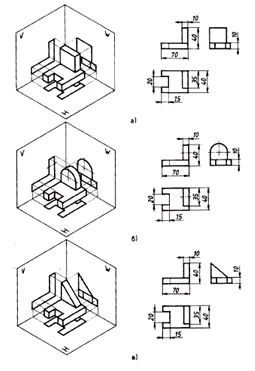
サイズ:
- 正面投影では –
結論: これは、図面の作成方法を学ぶには、オブジェクトを平面に投影できる必要があることを意味します。
定義テキスト内の不足している単語を埋めます。
1. _______________ と _______________ の投影があります。
2. _______________ 光線が 1 点から出ている場合、投影は _______________ と呼ばれます。
3. _______________ 光線が平行に向けられている場合、投影は _______________ と呼ばれます。
4. _______________ 光線が互いに平行で、投影面に対して 90 ° の角度で方向付けられている場合、その投影は _______________ と呼ばれます。
5. 投影面上の物体の自然な画像は、_____________ 投影によってのみ得られます。
6. 突起は互いに相対的に配置されています_______________。
7. 長方形投影法の創始者は_____________です
タスク 2. 研究プロジェクト
数字で示された主な種類と文字で示された部分を対応させて、答えをノートに記入してください。
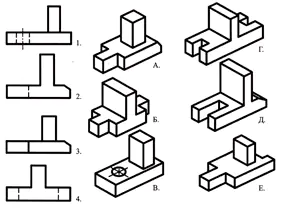
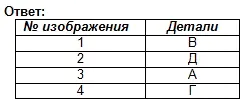
幾何体の知識を復習するための演習です。
口頭での説明を使用して、部品の視覚的なイメージを見つけます。
部品の底面は直方体の形状をしており、その小さい面には正四角柱状の溝が刻まれています。直方体の上面の中心には円錐台があり、その軸に沿って円筒状の貫通穴があります。
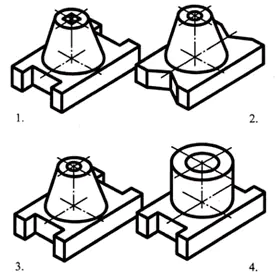
答え: パート No.3 (1点)
部品の技術図面とその正面投影 (投影の方向は矢印でマークされています) の間の対応を見つけます。散らばった図面イメージを基に、各パーツを 3 つのイメージからなる図面を作成します。答えを表に記入してください (図 129)。
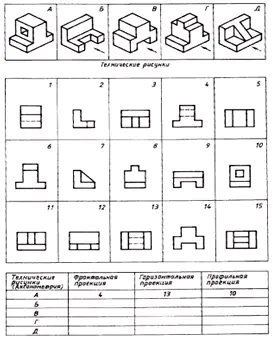
| 技術図面 | 正面投影 | 水平投影 | プロファイル投影 |
| あ | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| で | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
Ⅲ.実践的な作業。
タスクその1。研究プロジェクト
この視覚イメージの正面投影と水平投影を見つけます。答えをノートに書きましょう。
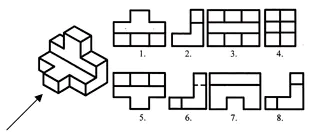
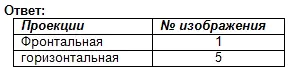
レッスンでの作業の評価。セルフテスト。 (プレゼンテーション2)
作品の最初の部分を採点するためのポイントがボードに書かれています。
タスクその2。クリエイティブな作業とその実装の検証
(クリエイティブプロジェクト)
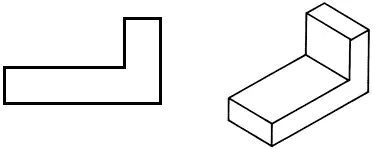
• ワークブックに正面投影図を描画します。
• 水平方向の投影を描き、質量を減らすために部品の形状を変更します。
• 必要に応じて、正面投影を変更します。
• 課題の完了を確認するには、1 人か 2 人の生徒を黒板に呼んで、問題の解決策を説明してもらいます。
IV.レッスンをまとめます。
1. レッスンでの作業の評価。 (実務部分の確認)
V. 宿題。
1. 研究プロジェクト。
表に従って作業します。番号で指定されたどの図面が、文字で指定された図面に対応するかを決定します。
投影方向が投影面に対して垂直である平行投影の特殊なケースを、と呼びます。 長方形 または 直交投影。 点の長方形 (直交) 投影は、その点から投影面に引いた垂線の底辺になります。点 A と点 B の長方形の投影を図に示します。 5.
平行投影から空間内の点の位置を決定するには、2 つの投影方向で取得された 2 つの平行な平面が必要です。
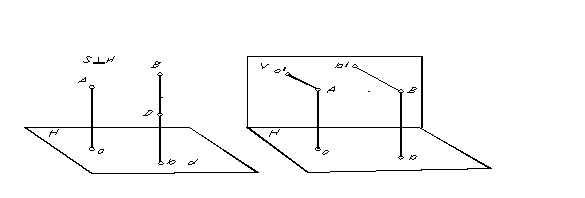 |
なぜなら点を通る場合、その平面に垂直な直線は 1 本しか描画できません。その場合、当然のことですが、直交投影では、1 つの点の 2 つの投影を取得するには、2 つの非平行な投影面が必要になります (図 6)。 。
正投影には、中心投影や平行投影に比べて多くの利点があります。これらには主に次のものが含まれます。
1. 点の正射影を決定するためのグラフィック構造の単純さ。
2. 特定の条件下で、投影上に投影された図形の形状とサイズを保存する機能。
注目された利点により、技術、特に機械工学図面の作成において、直交投影が広く使用されるようになりました。
機械工学では、描かれた物体の形状や大きさを図面から判断できるようにするために、図面を作成する際には、原則として 2 つではなく、複数の投影面を使用します。
空間内の点の位置、つまり任意の幾何学的図形の位置は、座標参照系が指定されていれば決定できます。投影面は空間を 8 つの部分 (八分円) に分割します。通常、それらにはローマ数字が付けられます (図 7)。
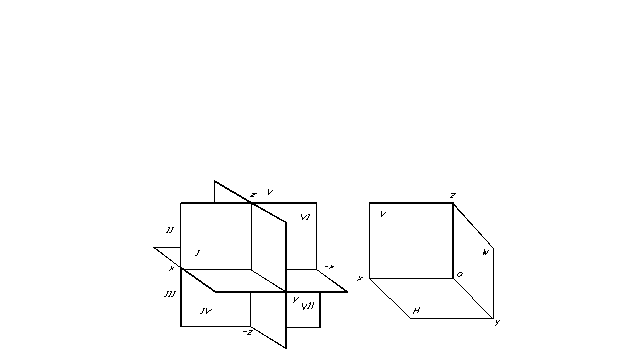
投影面は空間を 8 つの部分 (八分円) に分割します。通常、それらにはローマ数字が付けられます (図 7)。
空間内の幾何学的図形の位置を固定し、正投影からその形状を識別するのに最も便利なのは、3 つの相互に垂直な投影面で構成されるデカルト座標系です。記述幾何学は理論的研究の結果を実用に伝えるように設計されているため、3 つの投影面のシステムでも正投影を考慮することをお勧めします。
投影を容易にするために、3 つの相互に垂直な平面が 3 つの投影面として選択されます (図 8)。そのうちの 1 つは通常水平に配置されます - と呼ばれます 水平投影面、 もう 1 つは垂直で、図面平面に平行であり、と呼ばれます。 投影の前面面 そして 3 つ目は、既存の 2 つに対して垂直です - それはと呼ばれます 投影のプロファイル面。 これらの投影面は、と呼ばれる線に沿って交差します。 投影軸。
投影面の配置には右手系を採用しています。この場合、軸の正の方向が考慮されます。 バツ (水平投影面と正面投影面の交点) – 軸の原点の左側 y (水平投影面と側面投影面の交点) – 軸については、正面投影面から観察者に向かって z (投影の正面と側面の交点) – 投影の水平面から上方向、軸の反対方向は負とみなされます。
点の投影は、その点から対応する投影面上に引かれた垂線の底辺です。 水平投影 点は、水平投影面上の点の長方形の投影です。 正面投影 – それぞれ投影の前面と プロフィール – 投影のプロファイル面上。
この空間レイアウトを使用して幾何学的図形の正射影を描くのは、そのかさばり、また個々の図形 (水平方向と横方向) では投影された図形の形状とサイズが歪むため不便です。したがって、図面で空間レイアウトを描く代わりに、幾何学的図形の 3 つの相互接続された正投影から構成される複雑な図面 (モンジュ図) を使用します。
空間レイアウトの図への変換は、水平投影面と横投影面を正面投影面と組み合わせることで実行されます (図 7)。
平面には境界がないため、組み合わせた位置(図上)では平面の境界は表示されず、投影面の位置を示す刻印を残す必要はありません(図10)。
図に切り替えると、空間の明瞭さが失われます。この図は、構造を簡素化しながら、画像の測定の正確さと容易さをさらに提供します。しかし、空間像を想像するには想像力が必要です。
探しているものが見つかりませんでしたか?検索を使用します。
最高の名言: 学生にとって最も重要なことは、試験に合格することではなく、時間内に試験を思い出すことです。 9744 — | 7364 - またはすべて読みます。
投影図(記述幾何学の基礎)
投影法
長方形投影法
投影する光線が投影面と直角をなす場合、そのような投影は次のように呼ばれます。 長方形.
長方形投影とも呼ばれます。 直交。 「直交」という言葉は、ギリシャ語の「オルトス」(直線)と「ゴニア」(角度)に由来しています。
長方形投影法で描画すると、オブジェクトの形状とサイズの全体像が得られます。不等角投影法よりも実行が簡単です。
図面を正常に完成させるために知っておくべきことは何ですか?
平らな表面を持つオブジェクトは、頂点、エッジ、面によって制限されます (図 108)。したがって、図面でさまざまなオブジェクトを描画する方法を学ぶには、オブジェクトの頂点 (点)、エッジ (直線のセグメント)、およびオブジェクトのエッジ (平面の一部) が長方形の投影でどのように描画されるかを知る必要があります。
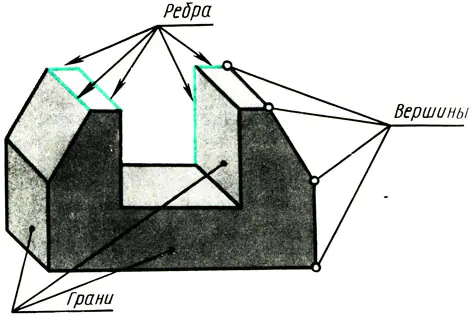
米。 108. 一連の点としてのプレムシュを書きます。平面の頂点
簡単な実験をしてみましょう。平らなオブジェクトと 100 個の要素がさまざまな位置でどのように描かれるかを見てみましょう。
窓の反対側の壁を投影面として考えます。窓の外に出しましょう 垂直 光線が壁に当たり、光線を投影します。厚い ABCD 紙を壁の前に (壁と平行に) 置きます (図 109、a)。壁には物体の投影に相当する影が形成されます。寸法はどのくらいですか?この場合、投影 a'b'c'd は、形状とサイズが投影のオブジェクトであるシートに対応します。
あいうえお。投影光線が投影面に対して垂直であるため、投影方法は長方形になります。
描かれたオブジェクトが、たとえばその高さ、つまりエッジ AD を中心に回転すると、投影はどのように変化しますか (図 109、b)。
回転すると、影の幅が縮小します(図 109 の線 a'b' と c'd'、b が短くなります)。紙のシートを回転し続けると、壁に垂直な位置では、シートの画像が線に変わりますが(図109、c)、オブジェクトの高さは一定のまま、つまり線a'に変わります。長さに沿った d' と b'c' は歪みません。
ここで、投影面に対して異なる位置にある長方形の投影において、平らなオブジェクトがどのような形状とサイズの画像を持つかについての結論を定式化しましょう。
a) 投影面に平行な平面図が自然なサイズで投影面上に描かれます (図 109、a)。
b)投影面に対して傾斜した平らな図形が、寸法の歪みを伴ってその上に描かれます(図109、b)。
c) 投影面に垂直な平面図が直線セグメントの形で投影面に描かれます (図 109、c)。
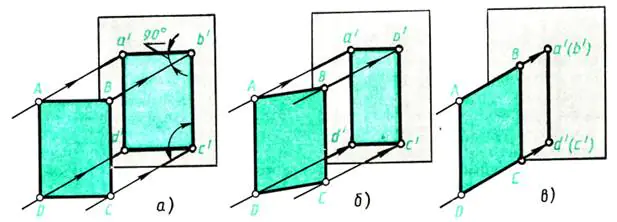
米。 109. 平面図形の投影
これらの発見は、オブジェクトのエッジの描写に関連しています。
長方形の投影では、オブジェクトのエッジ、つまり線はどのように描画されますか?
平らなオブジェクトを回転させて実験を繰り返し、そのエッジ、つまり線がどのように投影されるかを観察して、結論を導き出しましょう。
a) 投影面に平行な直線セグメントが自然なサイズで投影面上に描画されます (図 109、a、b、c のオブジェクト AD および BC の高さを、その投影 a'd' および b'c と比較してください。図 109 の a) の投影 a'b' および c'd' を含むオブジェクト AB および CD の幅。
b) 投影面に対して傾斜した直線セグメントは、長さが歪んで投影面上に描画されます (図 109、b のオブジェクト AB および CD の幅をその投影 a'b' および c'd' と比較してください)。
c) 投影面に垂直な直線セグメントは、その上の点によって描かれます (図 109 を参照、オブジェクトの幅を横切る、投影面に垂直な線 AB および CD)。
点の投影は、空間内の特定の点から投影面に下ろした垂線の底辺です (点 a’、b’、c’、d’ - 点 A、B、C、D の投影を参照)。
空間内の点を大文字の A、B、C、D などで表し、点の投影を対応する小文字の i、b、c、d などで表すことに同意しましょう。
図面内で一致する 2 つの点 (図 109、c) のうち、1 つは目に見える頂点のイメージであり、もう 1 つは目に見えない (閉じた) 頂点のイメージです。目に見えない頂点の投影の指定は括弧で囲まれています。



