Abschnitte: Technologie
Ziele und Zielsetzungen des Unterrichts:
lehrreich: Zeigen Sie den Schülern, wie sie beim Erstellen einer Zeichnung die rechteckige Projektionsmethode verwenden.
• die Notwendigkeit, drei Projektionsebenen zu verwenden;
• Bedingungen für die Ausbildung von Fähigkeiten schaffen, um ein Objekt auf drei Projektionsebenen zu projizieren;
Entwicklung: räumliche Konzepte, räumliches Denken, kognitives Interesse und kreative Fähigkeiten der Schüler entwickeln;
erziehen: Verantwortungsvoller Umgang mit dem Zeichnen, Pflege einer Kultur des grafischen Arbeitens.
Methoden und Techniken des Unterrichts: Erklärung, Gespräch, Problemsituationen, Recherche, Übungen, Frontalarbeit mit der Klasse, kreatives Arbeiten.
Materielle Unterstützung: Computer, Präsentation „Rechteckprojektion“, Aufgaben, Übungen, Übungskarten, Präsentation zum Selbsttest.
Unterrichtsart: Unterricht zur Wissensfestigung.
Wortschatzarbeit: horizontale Ebene, Projektion, Projektion, Profil, Forschung, Projekt.
I. Organisatorischer Teil.
Geben Sie das Thema und den Zweck der Lektion an.
Lasst uns ausführen Unterrichtswettbewerb, für jede Aufgabe erhalten Sie eine bestimmte Anzahl an Punkten. Abhängig von der erreichten Punktzahl wird eine Note für die Lektion vergeben.
II. Überblick über die Projektion und ihre Typen.
Projektion ist der mentale Prozess der Konstruktion von Bildern von Objekten auf einer Ebene.
Die Wiederholung erfolgt mittels Präsentation.
1. Studierende sind gefragt problematische Situation. (Präsentation 1)
Analysieren Sie die geometrische Form des Teils in der Frontprojektion und finden Sie dieses Teil in den visuellen Bildern.

Aus dieser Situation wird geschlossen, dass alle 6 Teile die gleiche Frontalprojektion haben. Dies bedeutet, dass eine Projektion nicht immer ein vollständiges Bild der Form und des Designs des Teils liefert.
- Was ist der Ausweg aus dieser Situation? (Betrachten Sie das Teil von der anderen Seite).
2. Es bestand die Notwendigkeit, eine andere Projektionsebene zu verwenden. (Horizontale Projektion).
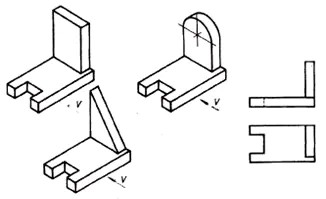
3. Die Notwendigkeit einer dritten Projektion entsteht, wenn zwei Projektionen nicht ausreichen, um die Form eines Objekts zu bestimmen.
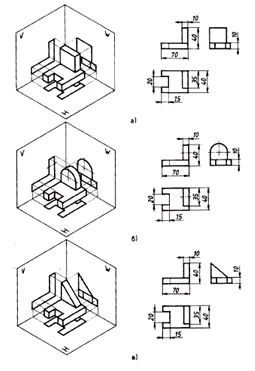
Größe:
- auf der Frontalprojektion –
Fazit: Das bedeutet, dass man zum Erlernen des Zeichnens in der Lage sein muss, Objekte auf eine Ebene zu projizieren.
Ergänzen Sie die fehlenden Wörter im Definitionstext.
1. Es gibt _______________- und ______________-Projektionen.
2. Wenn ______________ Strahlen von einem Punkt ausgehen, wird die Projektion als ______________ bezeichnet.
3. Wenn ______________ Strahlen parallel gerichtet sind, nennt man die Projektion _____________.
4. Wenn ______________ Strahlen parallel zueinander und in einem Winkel von 90° zur Projektionsebene gerichtet sind, dann heißt die Projektion ______________.
5. Ein natürliches Bild eines Objekts auf einer Projektionsebene erhält man nur mit ______________-Projektion.
6. Die Projektionen sind relativ zueinander angeordnet______________________________.
7. Der Begründer der rechteckigen Projektionsmethode ist _______________
Aufgabe 2. Forschungsprojekt
Ordnen Sie die durch Zahlen gekennzeichneten Haupttypen den durch Buchstaben gekennzeichneten Teilen zu und schreiben Sie die Antwort in Ihr Notizbuch.
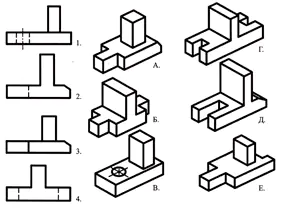
Eine Übung zur Überprüfung des Wissens über geometrische Körper.
Finden Sie anhand der verbalen Beschreibung ein visuelles Bild des Teils.
Die Basis des Teils hat die Form eines rechteckigen Parallelepipeds, dessen kleinere Flächen Rillen in Form eines regelmäßigen viereckigen Prismas aufweisen. In der Mitte der Oberseite des Parallelepipeds befindet sich ein Kegelstumpf, entlang dessen Achse sich ein durchgehendes zylindrisches Loch befindet.
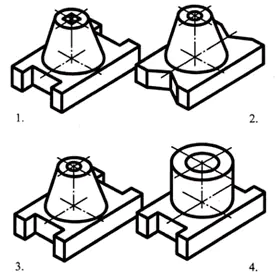
Antwort: Teil Nr. 3 (1 Punkt)
Finden Sie die Übereinstimmung zwischen den technischen Zeichnungen der Teile und ihren Frontalprojektionen (die Projektionsrichtung ist mit einem Pfeil markiert). Erstellen Sie anhand der verstreuten Bilder der Zeichnung eine Zeichnung jedes Teils, bestehend aus drei Bildern. Tragen Sie Ihre Antwort in die Tabelle ein (Abb. 129).
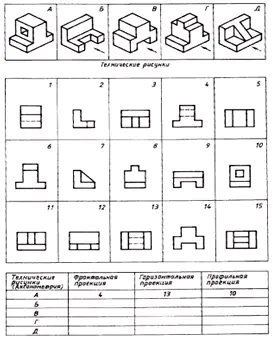
| Technische Zeichnungen | Frontalprojektion | Horizontale Projektion | Profilprojektion |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| IN | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktische Arbeit.
Aufgabe Nr. 1. Forschungsprojekt
Finden Sie die Frontal- und Horizontalprojektionen für dieses visuelle Bild. Schreiben Sie die Antwort in Ihr Notizbuch.
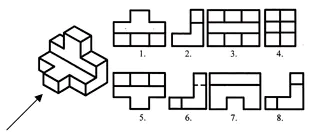
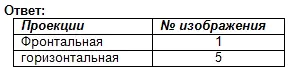
Beurteilung der Arbeit im Unterricht. Selbsttest. (Präsentation 2)
Die Punkte zur Bewertung des ersten Teils der Arbeit werden an die Tafel geschrieben:
Aufgabe Nr. 2. Kreative Arbeit und Überprüfung ihrer Umsetzung
(kreatives Projekt)
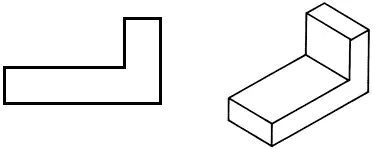
• Zeichnen Sie die Frontalprojektion in Ihr Arbeitsbuch ein.
• Zeichnen Sie eine horizontale Projektion und ändern Sie dabei die Form des Teils, um seine Masse zu reduzieren.
• Nehmen Sie bei Bedarf Änderungen an der Frontalprojektion vor.
• Um die Erledigung der Aufgabe zu überprüfen, rufen Sie einen oder zwei Schüler an die Tafel, um ihnen ihre Lösung für das Problem zu erläutern.
IV. Zusammenfassung der Lektion.
1. Beurteilung der Unterrichtsarbeit. (Überprüfung des praktischen Teils der Arbeit)
V. Hausaufgabe.
1. Forschungsprojekt.
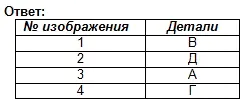
Arbeiten Sie nach der Tabelle: Bestimmen Sie, welche mit einer Zahl bezeichnete Zeichnung der mit einem Buchstaben bezeichneten Zeichnung entspricht.
Ein Sonderfall der Parallelprojektion, bei der die Projektionsrichtung senkrecht zur Projektionsebene verläuft, heißt rechteckig oder orthogonale Projektion. Die rechteckige (orthogonale) Projektion eines Punktes ist die Basis der Senkrechten, die vom Punkt zur Projektionsebene gezogen wird. Die rechteckige Projektion der Punkte A und B ist in Abb. dargestellt. 5.
Um die Position eines Punktes im Raum aus seinen Parallelprojektionen zu bestimmen, ist es notwendig, zwei parallele Ebenen in zwei Projektionsrichtungen zu erhalten.
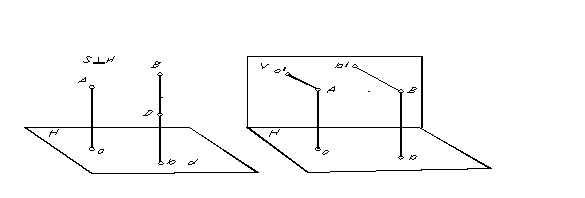 |
Weil Durch einen Punkt kann nur eine gerade Linie senkrecht zur Ebene gezeichnet werden. Um zwei Projektionen eines Punktes zu erhalten, sind bei einer orthogonalen Projektion offensichtlich zwei nichtparallele Projektionsebenen erforderlich (Abb. 6). .
Die orthographische Projektion hat gegenüber der Zentral- und Parallelprojektion eine Reihe von Vorteilen. Hierzu zählen vor allem:
1. Einfachheit grafischer Konstruktionen zur Bestimmung orthogonaler Projektionen von Punkten.
2. Die Fähigkeit, unter bestimmten Bedingungen die Form und Größe der projizierten Figur auf Projektionen beizubehalten.
Die genannten Vorteile haben dazu geführt, dass die Orthogonalprojektion in der Technik, insbesondere bei der Erstellung von Maschinenbauzeichnungen, weit verbreitet ist.
Um im Maschinenbau anhand einer Zeichnung die Form und Größe der abgebildeten Objekte beurteilen zu können, werden bei der Erstellung von Zeichnungen in der Regel nicht zwei, sondern mehrere Projektionsebenen verwendet.
Die Position eines Punktes im Raum und damit jeder geometrischen Figur kann bestimmt werden, wenn ein beliebiges Koordinatenbezugssystem angegeben wird. Projektionsebenen unterteilen den Raum in acht Teile – Oktanten. Sie werden herkömmlicherweise mit römischen Ziffern nummeriert (Abb. 7).
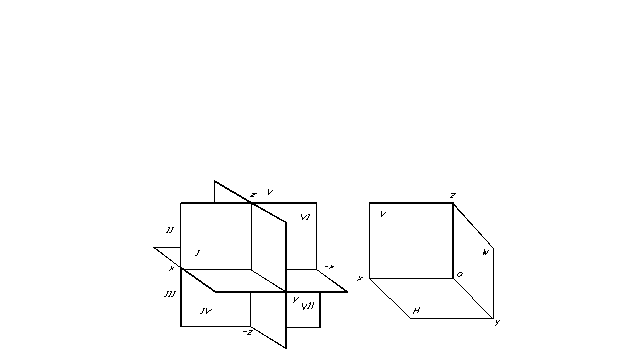
Projektionsebenen unterteilen den Raum in acht Teile – Oktanten. Sie werden herkömmlicherweise mit römischen Ziffern nummeriert (Abb. 7).
Am bequemsten lässt sich die Position einer geometrischen Figur im Raum festlegen und ihre Form anhand orthogonaler Projektionen identifizieren. Das kartesische Koordinatensystem besteht aus drei zueinander senkrechten Projektionsebenen. Da die beschreibende Geometrie darauf ausgelegt ist, die Ergebnisse ihrer theoretischen Forschung in die Praxis umzusetzen, empfiehlt es sich, die orthogonale Projektion auch in einem System von drei Projektionsebenen zu betrachten.
Zur Vereinfachung der Projektion werden drei zueinander senkrechte Ebenen als drei Projektionsebenen gewählt (Abb. 8). Einer von ihnen wird normalerweise horizontal platziert – so heißt es horizontale Projektionsebene, der andere ist vertikal, parallel zur Zeichenebene, heißt es frontale Projektionsebene und ein dritter, senkrecht zu den beiden vorhandenen - so heißt es Profilebene der Projektionen. Diese Projektionsebenen schneiden sich entlang der sogenannten Linien Projektionsachsen.
Wir haben ein rechtshändiges System zum Anordnen von Projektionsebenen übernommen. Dabei werden die positiven Richtungen der Achsen berücksichtigt: für die Achse X (Schnittpunkt der horizontalen und frontalen Projektionsebene) – links vom Ursprung, für die Achse j (Schnittpunkt der Horizontal- und Profilprojektionsebene) – von der Frontalprojektionsebene zum Betrachter hin, für die Achse z (Schnittpunkt der Frontal- und Profilebene der Projektionen) – Von der horizontalen Projektionsebene nach oben gelten die entgegengesetzten Richtungen der Achsen als negativ.
Die Projektion eines Punktes ist die Basis der Senkrechten, die von dem Punkt auf die entsprechende Projektionsebene gezogen wird. Horizontale Projektion Punkte sind die rechteckige Projektion eines Punktes auf einer horizontalen Projektionsebene, Frontalprojektion – jeweils auf der Frontalebene der Projektionen und Profil - auf der Profilebene der Projektionen.
Es ist unpraktisch, dieses räumliche Layout zur Darstellung orthogonaler Projektionen geometrischer Figuren zu verwenden, da es sperrig ist und auch aufgrund der Tatsache, dass bei einzelnen (horizontalen und im Profil) Form und Größe der projizierten Figur verzerrt sind. Anstatt eine räumliche Anordnung in einer Zeichnung darzustellen, verwenden sie daher eine komplexe Zeichnung (Monge-Diagramm), die aus drei miteinander verbundenen orthogonalen Projektionen einer geometrischen Figur besteht.
Die Umwandlung des räumlichen Grundrisses in Diagramme erfolgt durch Kombination der Horizontal- und Profilprojektionsebene mit der Frontalprojektionsebene (Abb. 7).
Da die Ebenen keine Grenzen haben, werden in der kombinierten Position (im Diagramm) die Grenzen der Ebenen nicht angezeigt, es ist nicht erforderlich, Beschriftungen zu hinterlassen, die die Position der Projektionsebenen angeben (Abb. 10).
Beim Wechsel zum Diagramm ging die räumliche Klarheit verloren. Das Diagramm bietet mehr – Genauigkeit und einfache Messung von Bildern bei einfacher Konstruktion. Um sich jedoch ein räumliches Bild vorzustellen, ist die Arbeit der Vorstellungskraft erforderlich.
Haben Sie nicht gefunden, was Sie gesucht haben? Nutzen Sie die Suche:
Beste Sprüche: Für einen Studierenden ist es nicht das Wichtigste, die Prüfung zu bestehen, sondern sich rechtzeitig daran zu erinnern. 9744 — | 7364 - oder alles lesen.
Projektionszeichnen (Grundlagen der Darstellenden Geometrie)
Projektionsmethode
Rechteckige Projektionsmethode
Wenn die projizierten Strahlen mit der Projektionsebene einen rechten Winkel bilden, nennt man solche Projektionen rechteckig.
Rechteckige Projektionen werden auch genannt senkrecht. Das Wort „orthogonal“ kommt von den griechischen Wörtern „ortos“ – gerade und „gonia“ – Winkel.
Zeichnungen im System rechteckiger Projektionen geben ein vollständiges Bild der Form und Größe des Objekts. Sie sind einfacher durchzuführen als axonometrische Projektionen.
Was müssen Sie wissen, um Zeichnungen erfolgreich fertigzustellen?
Jedes Objekt mit ebenen Oberflächen wird durch Scheitelpunkte, Kanten und Flächen begrenzt (Abb. 108). Um zu lernen, wie man verschiedene Objekte in Zeichnungen darstellt, müssen Sie daher wissen, wie Scheitelpunkte (Punkte), Kanten (Segmente gerader Linien) und Kanten von Objekten (Teile einer Ebene) in rechteckigen Projektionen dargestellt werden.
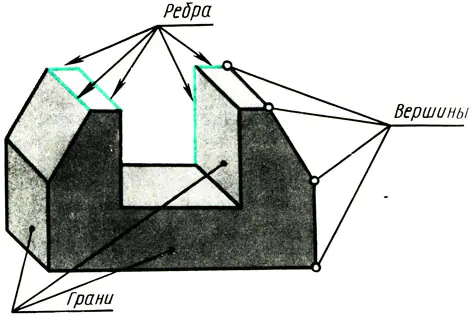
Reis. 108. Premsch als Punktemenge, schreiben. Eckpunkte von Flugzeugen
Machen wir ein einfaches Experiment. Sehen wir uns an, wie ein flaches Objekt und hundert Elemente in verschiedenen Positionen dargestellt werden.
Nehmen wir als Projektionsebene die Wand gegenüber dem Fenster. Lass es aus dem Fenster aufrecht Lichtstrahlen fallen auf die Wand – projizierende Strahlen. Legen Sie ein Blatt dickes ABCD-Papier vor die Wand (parallel dazu) (Abb. 109, a). An der Wand entsteht ein Schatten, der der Projektion des Objekts entspricht. Welche Abmessungen hat es? In diesem Fall entspricht die Projektion a’b’c’d’ in Form und Größe dem Projektionsobjekt – dem Blatt
A B C D. Die Projektionsmethode ist rechteckig, da die projizierten Strahlen senkrecht zur Projektionsebene stehen.
Wie verändert sich die Projektion, wenn das abgebildete Objekt beispielsweise um seine Höhe gedreht wird – Kante AD (Abb. 109, b)?
Beim Drehen wird der Schatten kleiner (die Linien a’b’ und c’d’ in Abb. 109, b werden kürzer). Wenn wir das Blatt Papier weiter drehen, stellen wir fest, dass sich das Bild des Blattes in einer Position senkrecht zur Wand in eine Linie verwandelt (Abb. 109, c), die Höhe des Objekts jedoch konstant bleibt, d.h. Linien a' d' und b'c' entlang der Länge werden nicht verzerrt.
Lassen Sie uns nun Schlussfolgerungen darüber formulieren, welche Form und Größe die Bilder eines flachen Objekts in rechteckigen Projektionen haben, die sich in Bezug auf die Projektionsebene unterschiedlich befinden:
a) Darauf ist eine flache Figur parallel zur Projektionsebene in natürlicher Größe abgebildet (Abb. 109, a);
b) Darauf ist eine flache, zur Projektionsebene geneigte Figur mit Dimensionsverzerrung abgebildet (Abb. 109, b);
c) Darauf ist eine flache Figur senkrecht zur Projektionsebene in Form eines geraden Liniensegments abgebildet (Abb. 109, c).
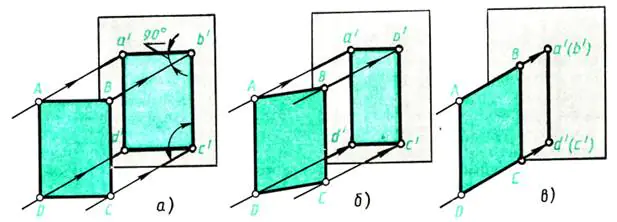
Reis. 109. Eine flache Figur projizieren
Diese Erkenntnisse beziehen sich auf die Darstellung der Kanten von Objekten.
Wie werden die Kanten von Objekten, also Linien, in rechteckigen Projektionen dargestellt?
Wiederholen wir das Experiment mit der Drehung eines flachen Objekts, beobachten wir, wie seine Kanten, also Linien, projiziert werden, und ziehen Schlussfolgerungen:
a) Darauf ist ein zur Projektionsebene paralleles Geradensegment in natürlicher Größe abgebildet (vergleiche die Höhe des Objekts AD und BC in Abb. 109, a, b, c mit seinen Projektionen a'd' und b'c, und die Breite des Objekts AB und CD mit seinen Projektionen a'b' und c'd' in Abb. 109, a);
b) Darauf ist ein zur Projektionsebene geneigtes gerades Segment mit einer Längenverzerrung dargestellt (vergleiche die Breite des Objekts AB und CD in Abb. 109, b mit seinen Projektionen a’b’ und c’d’);
c) Ein gerades Liniensegment senkrecht zur Projektionsebene wird durch einen Punkt darauf dargestellt (siehe in Abb. 109, über die Breite des Objekts - Linien AB und CD, senkrecht zur Projektionsebene).
Die Projektion eines Punktes ist die Basis einer Senkrechten, die von einem bestimmten Punkt im Raum auf die Projektionsebene abgesenkt wird (siehe Punkte a’, b’, c’, d’ – Projektionen der Punkte A, B, C, D).
Lassen Sie uns vereinbaren, Punkte im Raum mit den Großbuchstaben A, B, C, D usw. und Projektionen von Punkten mit den entsprechenden Kleinbuchstaben i, b, c, d usw. zu bezeichnen.
Von den beiden in der Zeichnung zusammenfallenden Punkten (Abb. 109, c) ist einer ein Bild eines sichtbaren Scheitelpunkts und der andere ein unsichtbarer (geschlossener) Scheitelpunkt. Die Bezeichnung der Projektionen unsichtbarer Eckpunkte ist in Klammern angegeben.



