Phần: Công nghệ
Mục đích và mục đích của bài học:
giáo dục: hướng dẫn học sinh cách sử dụng phương pháp chiếu hình chữ nhật khi vẽ;
• sự cần thiết phải sử dụng ba mặt phẳng chiếu;
• tạo điều kiện hình thành kỹ năng chiếu một vật thể lên ba mặt phẳng chiếu;
đang phát triển: phát triển khái niệm không gian, tư duy không gian, hứng thú nhận thức và khả năng sáng tạo của học sinh;
giáo dục: thái độ có trách nhiệm đối với việc vẽ, nuôi dưỡng văn hóa làm việc đồ họa.
Phương pháp và kỹ thuật giảng dạy: giải thích, đàm thoại, tình huống có vấn đề, nghiên cứu, bài tập, làm việc trước lớp, làm việc sáng tạo.
Hỗ trợ tài liệu: máy tính, thuyết trình “Hình chiếu chữ nhật”, bài tập, bài tập, phiếu bài tập, thuyết trình tự kiểm tra.
Loại bài học: bài học củng cố kiến thức.
Công việc từ vựng: mặt phẳng ngang, phép chiếu, phép chiếu, sơ đồ, nghiên cứu, dự án.
I. Bộ phận tổ chức.
Nêu chủ đề và mục đích của bài học.
Hãy thực hiện cuộc thi bài học, với mỗi nhiệm vụ bạn sẽ nhận được một số điểm nhất định. Tùy theo số điểm ghi được sẽ cho điểm cho bài học.
II. Xem xét phép chiếu và các loại của nó.
Phép chiếu là quá trình tinh thần xây dựng hình ảnh của các vật thể trên một mặt phẳng.
Sự lặp lại được thực hiện bằng cách sử dụng cách trình bày.
1. Học sinh được hỏi tình huống có vấn đề. (Trình bày 1)
Phân tích hình dạng hình học của phần trên hình chiếu phía trước và tìm phần này trong số các hình ảnh trực quan.

Từ tình huống này người ta kết luận rằng cả 6 phần đều có hình chiếu chính diện giống nhau. Điều này có nghĩa là một phép chiếu không phải lúc nào cũng đưa ra một bức tranh hoàn chỉnh về hình dạng và thiết kế của bộ phận.
- Làm cách nào để thoát khỏi tình trạng này? (Nhìn phần từ phía bên kia).
2. Cần phải sử dụng một mặt phẳng chiếu khác. (Hình chiếu ngang).
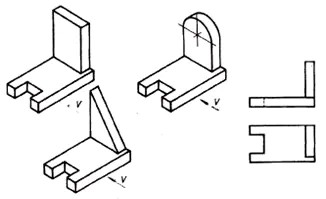
3. Nhu cầu về hình chiếu thứ ba nảy sinh khi hai hình chiếu không đủ để xác định hình dạng của một vật thể.
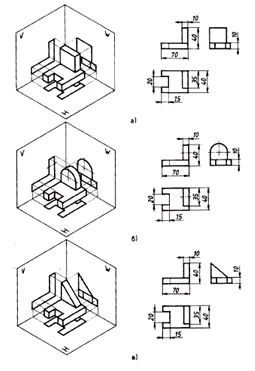
Định cỡ:
- trên hình chiếu phía trước –
Kết luận: điều này có nghĩa là để học cách vẽ, bạn cần có khả năng chiếu các vật thể lên một mặt phẳng.
Điền những từ còn thiếu vào văn bản định nghĩa.
1. Có hình chiếu _______________ và _______________.
2. Nếu tia ______________ phát ra từ một điểm thì phép chiếu được gọi là ______________.
3. Nếu tia ______________ hướng song song thì hình chiếu được gọi là _____________.
4. Nếu các tia ______________ hướng song song với nhau và hợp với mặt phẳng chiếu một góc 90° thì hình chiếu được gọi là ______________.
5. Chỉ có được ảnh tự nhiên của vật trên mặt phẳng chiếu bằng phép chiếu ______________.
6. Các hình chiếu được đặt tương đối với nhau______________________________.
7. Người sáng lập ra phương pháp chiếu hình chữ nhật là _______________
Nhiệm vụ 2. Đề tài nghiên cứu
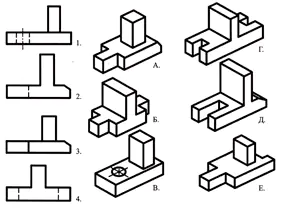
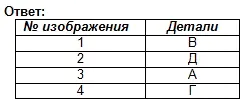
Ghép các loại chính được biểu thị bằng số với các phần được biểu thị bằng chữ cái và viết câu trả lời vào vở của bạn.
Bài tập ôn tập kiến thức về hình học.
Sử dụng mô tả bằng lời nói, tìm hình ảnh trực quan của bộ phận.
Phần đế của bộ phận có dạng hình chữ nhật song song, các mặt nhỏ hơn có các rãnh hình lăng trụ tứ giác đều. Ở trung tâm của mặt trên của hình bình hành có một hình nón cụt, dọc theo trục có một lỗ hình trụ xuyên qua.
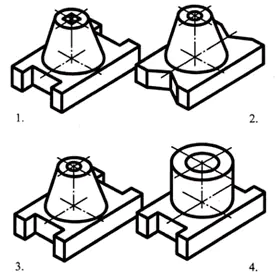
Đáp án: phần số 3 (1 điểm)
Tìm sự tương ứng giữa các bản vẽ kỹ thuật của các bộ phận và hình chiếu phía trước của chúng (hướng chiếu được đánh dấu bằng một mũi tên). Dựa trên các hình ảnh rải rác của bức vẽ, vẽ từng phần gồm ba hình ảnh. Viết câu trả lời của bạn vào bảng (Hình 129).
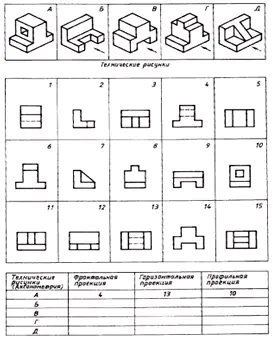
| Bản vẽ kỹ thuật | Hình chiếu phía trước | Chiếu ngang | Phép chiếu hồ sơ |
| MỘT | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| TRONG | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Công việc thực tế.
Nhiệm vụ số 1. Dự án nghiên cứu
Tìm các hình chiếu phía trước và ngang cho hình ảnh trực quan này. Viết câu trả lời vào sổ tay của bạn.
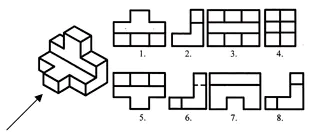
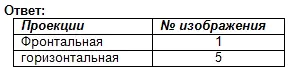
Đánh giá công việc trong bài học. Tự kiểm tra. (Trình bày 2)
Điểm chấm phần đầu tiên của tác phẩm được ghi trên bảng:
Nhiệm vụ số 2. Công việc sáng tạo và xác minh việc thực hiện nó
(dự án sáng tạo)
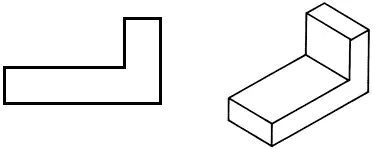
• Vẽ hình chiếu phía trước vào sổ làm việc của bạn.
• Vẽ hình chiếu ngang, thay đổi hình dạng của bộ phận để giảm khối lượng của nó.
• Nếu cần, hãy thay đổi hình chiếu phía trước.
• Để kiểm tra việc hoàn thành nhiệm vụ, gọi một hoặc hai học sinh lên bảng để giải thích cách giải của mình.
IV. Tóm tắt bài học.
1. Đánh giá công việc trong bài. (Kiểm tra phần thực hành của bài)
V. Giao bài tập về nhà.
1. Dự án nghiên cứu.
Làm việc theo bảng: xác định hình vẽ nào được ký hiệu bằng số tương ứng với hình vẽ được ký hiệu bằng chữ cái.
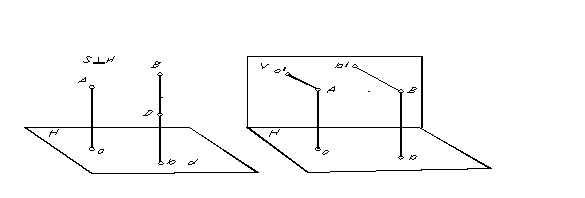
Trường hợp đặc biệt của phép chiếu song song, trong đó phương chiếu vuông góc với mặt phẳng chiếu được gọi là hình hộp chữ nhật hoặc phép chiếu trực giao. Hình chiếu chữ nhật (trực giao) của một điểm là đáy của đường vuông góc kẻ từ điểm đó lên mặt phẳng chiếu. Hình chiếu hình chữ nhật của các điểm A và B được thể hiện trên hình 2. 5.
Để xác định vị trí của một điểm trong không gian từ các hình chiếu song song của nó, cần có hai mặt phẳng song song thu được theo hai hướng chiếu.
 |
Bởi vì qua một điểm chỉ vẽ được một đường thẳng vuông góc với mặt phẳng, khi đó rõ ràng với phép chiếu trực giao, để thu được hai hình chiếu của một điểm thì cần phải có hai mặt phẳng chiếu không song song (Hình 6) .
Phép chiếu trực giao có một số ưu điểm so với phép chiếu tâm và song song. Chúng chủ yếu bao gồm:
1. Đơn giản hóa việc xây dựng đồ họa để xác định hình chiếu trực giao của điểm.
2. Khả năng, trong những điều kiện nhất định, giữ nguyên hình dạng và kích thước của hình chiếu trên hình chiếu.
Những ưu điểm được ghi nhận đã đảm bảo việc sử dụng rộng rãi phép chiếu trực giao trong công nghệ, đặc biệt là trong việc chuẩn bị các bản vẽ kỹ thuật cơ khí.
Trong kỹ thuật cơ khí, để có thể đánh giá hình dạng và kích thước của các vật thể được mô tả từ bản vẽ, khi vẽ bản vẽ, theo quy luật, người ta không sử dụng hai mà là một số mặt phẳng chiếu.
Vị trí của một điểm trong không gian, và do đó của bất kỳ hình hình học nào, có thể được xác định nếu bất kỳ hệ quy chiếu tọa độ nào được chỉ định. Các mặt phẳng chiếu chia không gian thành tám phần - octant. Chúng được đánh số theo quy ước bằng chữ số La Mã (Hình 7).
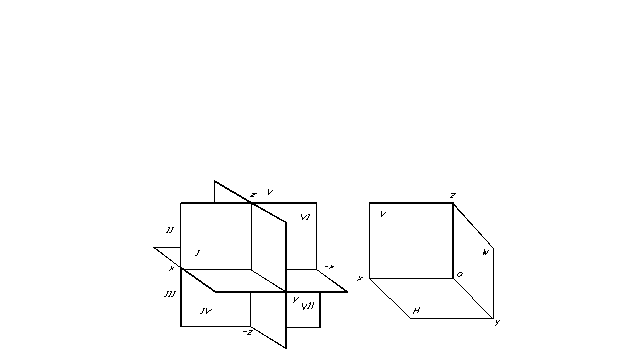
Các mặt phẳng chiếu chia không gian thành tám phần - octant. Chúng được đánh số theo quy ước bằng chữ số La Mã (Hình 7).
Thuận tiện nhất để cố định vị trí của một hình hình học trong không gian và xác định hình dạng của nó từ các hình chiếu trực giao là hệ tọa độ Descartes, bao gồm ba mặt phẳng chiếu vuông góc với nhau. Do hình học mô tả được thiết kế để truyền tải các kết quả nghiên cứu lý thuyết của nó vào sử dụng thực tế, nên cũng nên xem xét phép chiếu trực giao trong một hệ gồm ba mặt phẳng chiếu.
Để dễ chiếu, ba mặt phẳng vuông góc với nhau được chọn làm ba mặt phẳng chiếu (Hình 8). Một trong số chúng thường được đặt theo chiều ngang - nó được gọi là mặt phẳng chiếu ngang, cái kia thẳng đứng, song song với mặt phẳng vẽ, gọi là mặt phẳng phía trước của hình chiếu và cái thứ ba, vuông góc với hai cái hiện có - nó được gọi là mặt phẳng biên dạng của các hình chiếu. Các mặt phẳng chiếu này cắt nhau dọc theo các đường thẳng gọi là các trục chiếu.
Chúng tôi đã áp dụng hệ thống thuận tay phải để sắp xếp các mặt phẳng chiếu. Trong trường hợp này, chiều dương của các trục được xét: đối với trục X (giao điểm của mặt phẳng chiếu ngang và mặt phẳng chiếu) – ở bên trái gốc tọa độ, đối với trục y (giao điểm của mặt phẳng chiếu ngang và mặt cắt) – về phía người quan sát từ mặt phẳng chiếu phía trước, đối với trục z (Giao điểm của các mặt phẳng phía trước và mặt cắt của các hình chiếu) – hướng lên từ mặt phẳng ngang của các hình chiếu, các hướng ngược nhau của các trục được coi là âm.
Hình chiếu của một điểm là đáy của đường vuông góc kẻ từ điểm đó lên mặt phẳng chiếu tương ứng. Chiếu ngang điểm là hình chiếu hình chữ nhật của một điểm trên mặt phẳng chiếu ngang, chiếu chính diện – tương ứng trên mặt phẳng phía trước của hình chiếu và hồ sơ - trên mặt phẳng biên dạng của các hình chiếu.
Thật bất tiện khi sử dụng bố cục không gian này để mô tả các hình chiếu trực giao của các hình hình học do tính cồng kềnh của nó và cũng do trên các hình chiếu riêng lẻ (ngang và mặt cắt), hình dạng và kích thước của hình chiếu bị biến dạng. Do đó, thay vì mô tả bố cục không gian trong bản vẽ, họ sử dụng một bản vẽ phức tạp (sơ đồ Monge) bao gồm ba hình chiếu trực giao liên kết với nhau của một hình hình học.
Việc chuyển đổi bố cục không gian thành sơ đồ được thực hiện bằng cách kết hợp các mặt phẳng chiếu ngang và mặt cắt với mặt phẳng chiếu phía trước (Hình 7).
Vì các mặt phẳng không có ranh giới nên ở vị trí kết hợp (trên sơ đồ) ranh giới của các mặt phẳng không được hiển thị nên không cần phải để lại dòng chữ chỉ vị trí của các mặt phẳng chiếu (Hình 10).
Đã chuyển sang sơ đồ, sự rõ ràng về không gian đã bị mất. Sơ đồ mang lại nhiều hơn - độ chính xác và dễ dàng đo lường hình ảnh, với việc xây dựng đơn giản. Tuy nhiên, để tưởng tượng ra một bức tranh không gian đòi hỏi phải có trí tưởng tượng.
Không tìm thấy những gì bạn đang tìm kiếm? Sử dụng tìm kiếm:
Những câu nói hay nhất: Đối với một học sinh, điều quan trọng nhất không phải là vượt qua kỳ thi mà là ghi nhớ kịp thời. 9744 — | 7364 - hoặc đọc tất cả.
Vẽ hình chiếu (cơ bản về hình học mô tả)
Phương pháp chiếu
Phương pháp chiếu hình chữ nhật
Nếu tia chiếu vuông góc với mặt phẳng chiếu thì hình chiếu đó gọi là hình hộp chữ nhật.
Hình chiếu hình chữ nhật còn được gọi là trực giao. Từ "trực giao" xuất phát từ tiếng Hy Lạp "ortos" - thẳng và "gonia" - góc.
Hình vẽ theo hệ thống hình chiếu chữ nhật cho hình ảnh đầy đủ về hình dạng, kích thước của vật thể. Chúng dễ thực hiện hơn các phép chiếu trục đo.
Bạn cần biết những gì để hoàn thành bản vẽ thành công?
Bất kỳ vật thể nào có bề mặt phẳng đều bị giới hạn bởi các đỉnh, cạnh và mặt (Hình 108). Do đó, để học cách khắc họa các đối tượng khác nhau trong hình vẽ, bạn cần biết các đỉnh (điểm), các cạnh (đoạn của đường thẳng) và các cạnh của đối tượng (các phần của mặt phẳng) được thể hiện như thế nào trong các hình chiếu hình chữ nhật.
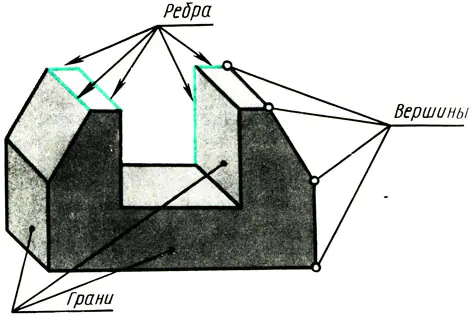
Cơm. 108. Premsch là tập hợp các điểm, hãy viết. Các đỉnh của mặt phẳng
Hãy làm một thí nghiệm đơn giản. Chúng ta hãy xem một vật thể phẳng và hàng trăm phần tử được mô tả ở các vị trí khác nhau như thế nào.
Chúng ta hãy lấy bức tường đối diện với cửa sổ làm mặt phẳng chiếu. Hãy để nó ra ngoài cửa sổ vuông góc Tia sáng chiếu vào tường - tia chiếu. Đặt một tờ giấy ABCD dày ở phía trước bức tường (song song với nó) (Hình 109, a). Một cái bóng được hình thành trên tường, tương đương với hình chiếu của vật thể. Kích thước của nó là gì? Trong trường hợp này, hình chiếu a’b’c’d’ có hình dạng và kích thước tương ứng với vật được chiếu - tấm
A B C D. Phương pháp chiếu là hình chữ nhật, vì các tia chiếu vuông góc với mặt phẳng chiếu.
Hình chiếu sẽ thay đổi như thế nào nếu đối tượng được mô tả được xoay, chẳng hạn như xung quanh chiều cao của nó - cạnh AD (Hình 109, b)?
Khi xoay, bóng sẽ co lại về chiều rộng (các đường a’b’ và c’d’ trong Hình 109, b trở nên ngắn hơn). Tiếp tục quay tờ giấy, ta lưu ý rằng ở vị trí vuông góc với tường thì ảnh của tờ giấy sẽ biến thành một đường thẳng (Hình 109, c), nhưng chiều cao của vật không đổi, tức là đường thẳng a' d' và b'c' dọc theo chiều dài không bị biến dạng.
Bây giờ chúng ta hãy đưa ra kết luận về hình dạng và kích thước của hình ảnh mà một vật thể phẳng có trong các hình chiếu hình chữ nhật, nằm ở các vị trí khác nhau so với mặt phẳng chiếu:
a) một hình phẳng song song với mặt phẳng chiếu được vẽ trên đó với kích thước tự nhiên (Hình 109, a);
b) một hình phẳng nghiêng với mặt phẳng chiếu được mô tả trên đó với sự biến dạng về kích thước (Hình 109, b);
c) một hình phẳng vuông góc với mặt phẳng chiếu được vẽ trên đó dưới dạng một đoạn thẳng (Hình 109, c).
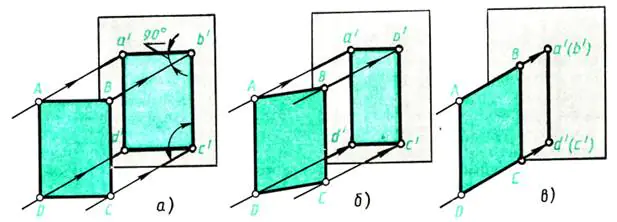
Cơm. 109. Chiếu hình phẳng
Những phát hiện này liên quan đến việc mô tả các cạnh của vật thể.
Các cạnh của vật thể, tức là các đường thẳng, được mô tả như thế nào trong hình chiếu hình chữ nhật?
Chúng ta hãy lặp lại thí nghiệm quay một vật phẳng, quan sát các cạnh của nó, tức là các đường thẳng, được chiếu như thế nào và rút ra kết luận:
a) Đoạn thẳng song song với mặt phẳng chiếu được vẽ trên đó với kích thước tự nhiên (so sánh chiều cao của vật AD và BC ở Hình 109, a, b, c với các hình chiếu a'd' và b'c, và chiều rộng của vật AB và CD với các hình chiếu a'b' và c'd' của hình 109, a);
b) một đoạn thẳng nghiêng với mặt phẳng chiếu được vẽ trên đó với độ biến dạng về chiều dài (so sánh chiều rộng của vật AB và CD trong Hình 109, b với các hình chiếu a'b' và c'd' của nó);
c) Đoạn thẳng vuông góc với mặt phẳng chiếu được vẽ bằng một điểm trên đó (xem Hình 109, ngang qua chiều rộng của vật - các đường thẳng AB và CD, vuông góc với mặt phẳng chiếu).
Hình chiếu của một điểm là đáy của đường vuông góc hạ từ một điểm cho trước trong không gian lên mặt phẳng chiếu (xem các điểm a’, b’, c’, d’ - hình chiếu của các điểm A, B, C, D).
Chúng ta hãy đồng ý biểu thị các điểm trong không gian bằng các chữ cái in hoa A, B, C, D, v.v. và hình chiếu của các điểm bằng các chữ cái viết thường tương ứng i, b, c, d, v.v.
Trong số hai điểm trùng nhau trong hình vẽ (Hình 109, c), một điểm là ảnh của một đỉnh nhìn thấy được, và điểm kia là ảnh vô hình (đóng). Việc chỉ định hình chiếu của các đỉnh vô hình được lấy trong ngoặc đơn.



