Avsnitt: Teknologi
Mål och mål med lektionen:
pedagogisk: visa eleverna hur man använder metoden rektangulär projektion när man gör en ritning;
• behovet av att använda tre projektionsplan;
• skapa förutsättningar för bildandet av färdigheter för att projicera ett objekt på tre projektionsplan;
utvecklande: utveckla rumsliga koncept, rumsligt tänkande, kognitivt intresse och kreativa förmågor hos elever;
utbilda: ansvarsfull inställning till teckning, att odla en kultur av grafiskt arbete.
Metoder och tekniker för undervisning: förklaring, samtal, problemsituationer, forskning, övningar, frontalarbete med klassen, kreativt arbete.
Materialstöd: datorer, presentation ”Rektangulär projektion”, uppgifter, övningar, övningskort, presentation för självtest.
Lektionstyp: lektion för att konsolidera kunskap.
Ordförrådsarbete: horisontellt plan, projektion, projektion, profil, forskning, projekt.
I. Organisatorisk del.
Ange ämnet och syftet med lektionen.
Låt oss genomföra lektion-tävling, för varje uppgift får du ett visst antal poäng. Beroende på poängen kommer ett betyg på lektionen att ges.
II. Genomgång av projektion och dess typer.
Projektion är den mentala processen att konstruera bilder av objekt på ett plan.
Repetition utförs med hjälp av presentation.
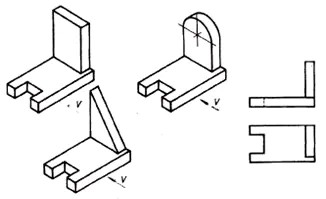
1. Eleverna tillfrågas problematisk situation. (Presentation 1)
Analysera den geometriska formen av delen på den främre projektionen och hitta denna del bland de visuella bilderna.

Från denna situation dras slutsatsen att alla 6 delarna har samma frontalprojektion. Detta gör att en projektion inte alltid ger en fullständig bild av delens form och design.
- Vad är vägen ut ur den här situationen? (Titta på delen från andra sidan).
2. Det fanns ett behov av att använda ett annat projektionsplan. (Horisontell projektion).
3. Behovet av en tredje projektion uppstår när två projektioner inte räcker för att bestämma formen på ett föremål.
Storlek:
- på frontalprojektionen –
Slutsats: detta betyder att för att lära sig att göra ritningar måste du kunna projicera objekt på ett plan.
Fyll i de ord som saknas i definitionstexten.
1. Det finns _______________ och ______________ projektion.
2. Om ______________ strålar kommer ut från en punkt kallas projektion ______________.
3. Om ______________ strålar riktas parallellt kallas projektion ________________.
4. Om ______________ strålar riktas parallellt med varandra och i en vinkel på 90° mot projektionsplanet, kallas projektionen ______________.
5. En naturlig bild av ett objekt på ett projektionsplan erhålls endast med ______________ projektion.
6. Projektionerna är placerade i förhållande till varandra______________________________.
7. Grundaren av den rektangulära projektionsmetoden är _______________
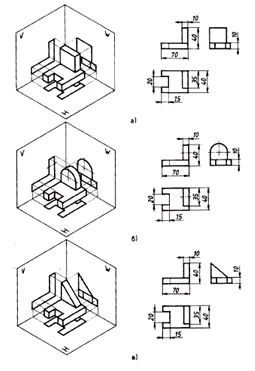
Uppgift 2. Forskningsprojekt
Matcha huvudtyperna som anges med siffror med delarna som anges med bokstäver och skriv svaret i din anteckningsbok.
En övning för att granska kunskap om geometriska kroppar.
Använd den verbala beskrivningen och hitta en visuell bild av delen.
Basen av delen har formen av en rektangulär parallellepiped, vars mindre ytor har spår i form av ett regelbundet fyrkantigt prisma. I mitten av parallellepipedens övre yta finns en stympad kon, längs vars axel det finns ett genomgående cylindriskt hål.
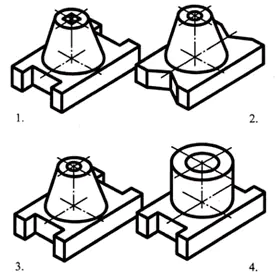
Svar: del nr 3 (1 poäng)
Hitta överensstämmelsen mellan de tekniska ritningarna av delarna och deras frontalprojektioner (projektionsriktningen är markerad med en pil). Baserat på de spridda bilderna av ritningen, gör en ritning av varje del, bestående av tre bilder. Skriv ditt svar i tabellen (bild 129).
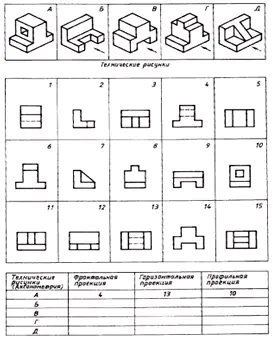
| Tekniska ritningar | Frontal projektion | Horisontell projektion | Profilprojektion |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| I | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktiskt arbete.
Uppgift nr 1. Forskningsrojekt
Hitta frontala och horisontella projektioner för denna visuella bild. Skriv svaret i din anteckningsbok.
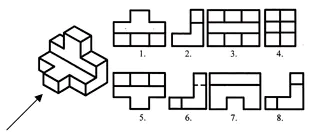
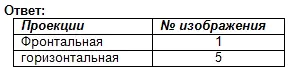
Bedömning av arbete på lektionen. Självtest. (Presentation 2)
Poängen för att betygsätta den första delen av arbetet skrivs på tavlan:
Uppgift nr 2. Kreativt arbete och verifiering av dess genomförande
(kreativt projekt)
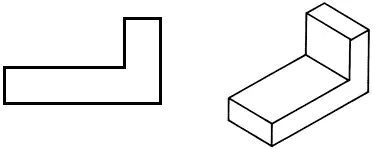
• Rita in frontprojektionen i din arbetsbok.
• Rita en horisontell projektion, ändra formen på delen för att minska dess massa.
• Vid behov, gör ändringar i frontalprojektionen.
• För att kontrollera att uppgiften är klar, ring en eller två elever till styrelsen för att förklara sin lösning på problemet.
IV. Sammanfattning av lektionen.
1. Bedömning av arbete på lektionen. (Kontrollerar den praktiska delen av arbetet)
V. Läxuppgift.
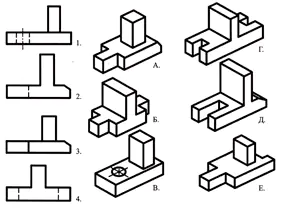
1. Forskningsprojekt.
Arbeta enligt tabellen: bestäm vilken ritning, betecknad med ett nummer, som motsvarar ritningen, betecknad med en bokstav.
Ett specialfall av parallell projektion, där projektionsriktningen är vinkelrät mot projektionsplanet, kallas rektangulär eller ortogonal projektion. Den rektangulära (ortogonala) projektionen av en punkt är basen av den vinkelräta som dras från punkten till projektionsplanet. Den rektangulära projektionen av punkterna A och B visas i fig. 5.
För att bestämma positionen för en punkt i rymden från dess parallella projektioner är det nödvändigt att ha två parallella plan erhållna i två projektionsriktningar.
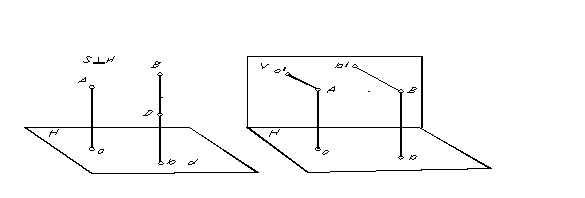 |
Därför att genom en punkt kan endast en rät linje vinkelrät mot planet dras, då är det uppenbarligen, med ortogonal projektion, för att få två projektioner av en punkt nödvändigt att ha två icke-parallella projektionsplan (Fig. 6). .
Ortografisk projektion har ett antal fördelar jämfört med central och parallell projektion. Dessa inkluderar främst:
1. Enkelhet av grafiska konstruktioner för att bestämma ortogonala projektioner av punkter.
2. Förmågan att under vissa förhållanden bevara formen och storleken på den projicerade figuren på projektioner.
De noterade fördelarna har säkerställt den utbredda användningen av ortogonal projektion inom teknik, i synnerhet för framställning av maskintekniska ritningar.
Inom maskinteknik, för att utifrån en ritning kunna bedöma formen och storleken på de avbildade föremålen, använder de i regel inte två, utan flera projektionsplan när de ritar ritningar.
Positionen för en punkt i rymden, och därför för vilken geometrisk figur som helst, kan bestämmas om något koordinatreferenssystem anges. Projektionsplan delar upp rymden i åtta delar - oktanter. De är konventionellt numrerade med romerska siffror (fig. 7).
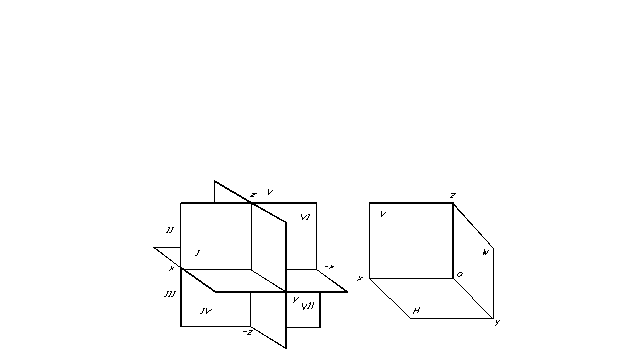
Projektionsplan delar upp rymden i åtta delar - oktanter. De är konventionellt numrerade med romerska siffror (fig. 7).
Det mest bekväma för att fixera positionen för en geometrisk figur i rymden och identifiera dess form från ortogonala projektioner är det kartesiska koordinatsystemet, som består av tre ömsesidigt vinkelräta projektionsplan. På grund av det faktum att beskrivande geometri är utformad för att förmedla resultaten av dess teoretiska forskning för praktisk användning, är det tillrådligt att överväga ortogonal projektion även i ett system med tre projektionsplan.
För att underlätta projiceringen väljs tre inbördes vinkelräta plan som tre projektionsplan (fig. 8). En av dem är vanligtvis placerad horisontellt - det kallas horisontellt projektionsplan, den andra är vertikal, parallell med ritningsplanet, kallas det frontalplan av projektioner och en tredje, vinkelrät mot de två befintliga - kallas det profilplan av projektioner. Dessa projektionsplan skär längs linjer som kallas projektionsaxlar.
Vi har antagit ett högerhänt system för att arrangera projektionsplan. I detta fall beaktas de positiva riktningarna för axlarna: för axeln X (korsning av horisontella och frontala projektionsplan) – till vänster om origo, för axeln y (korsning av horisontella och profilerade projektionsplan) – mot observatören från frontalprojektionsplanet, för axeln z (korsningen av projektionernas front- och profilplan) – uppåt från projektionernas horisontella plan anses axlarnas motsatta riktningar vara negativa.
Projektionen av en punkt är basen av den vinkelräta ritad från punkten till motsvarande projektionsplan. Horisontell projektion punkter är den rektangulära projektionen av en punkt på ett horisontellt projektionsplan, frontal projektion – respektive på frontalplanet av projektioner och profil – på projektionernas profilplan.
Det är obekvämt att använda denna rumsliga layout för att avbilda ortogonala projektioner av geometriska figurer på grund av dess skrymmande, och även på grund av det faktum att på individuella (horisontella och profiler) formen och storleken på den projicerade figuren är förvrängd. Därför, istället för att avbilda en rumslig layout i en ritning, använder de en komplex ritning (Monge-diagram) som består av tre sammankopplade ortogonala projektioner av en geometrisk figur.
Omvandlingen av den rumsliga layouten till diagram utförs genom att kombinera horisontal- och profilprojektionsplanen med frontprojektionsplanet (fig. 7).
Eftersom planen inte har några gränser, i den kombinerade positionen (på diagrammet) visas inte planens gränser, det finns inget behov av att lämna inskriptioner som indikerar projektionsplanens position (fig. 10).
Efter att ha bytt till diagrammet gick rumslig klarhet förlorad. Diagrammet ger mer - noggrannhet och enkel mätning av bilder, med enkel konstruktion. Men för att föreställa sig en rumslig bild krävs fantasiarbete.
Hittade du inte det du letade efter? Använd sökningen:
Bästa ordspråk: För en student är det viktigaste att inte klara provet, utan att komma ihåg det i tid. 9744 — | 7364 - eller läs allt.
Projektionsritning (grunderna för beskrivande geometri)
Projektionsmetod
Rektangulär projektionsmetod
Om de utskjutande strålarna bildar en rät vinkel med projektionsplanet, kallas sådana projektioner rektangulär.
Rektangulära projektioner kallas också ortogonal. Ordet "ortogonal" kommer från de grekiska orden "ortos" - rak och "gonia" - vinkel.
Ritningar i systemet med rektangulära projektioner ger en komplett bild av objektets form och storlek. De är lättare att utföra än axonometriska projektioner.
Vad behöver du veta för att framgångsrikt slutföra ritningar?
Alla föremål som har plana ytor begränsas av hörn, kanter och ytor (bild 108). Därför, för att lära dig hur man avbildar olika objekt i ritningar, måste du veta hur hörn (punkter), kanter (segment av räta linjer) och kanter på objekt (delar av ett plan) avbildas i rektangulära projektioner.
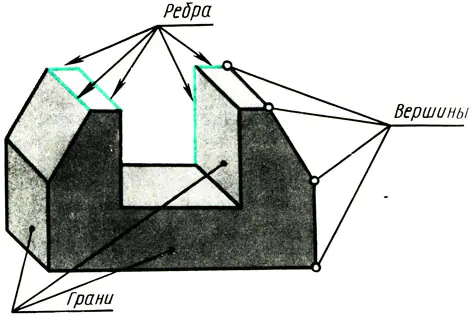
Ris. 108. Premsch som en uppsättning punkter, skriv. Vertices av plan
Låt oss göra ett enkelt experiment. Låt oss se hur ett platt föremål och hundra element avbildas i olika positioner.
Låt oss ta väggen mittemot fönstret som projektionsplan. Släpp ut det genom fönstret vinkelrät Ljusstrålar faller på väggen - utskjutande strålar. Placera ett ark tjockt ABCD-papper framför väggen (parallellt med den) (bild 109, a). En skugga bildas på väggen, motsvarande objektets projektion. Vilka är dess dimensioner? I det här fallet motsvarar projektionen a'b'c'd' i form och storlek objektet för projektionen - arket
ABCD. Projektionsmetoden är rektangulär, eftersom de utskjutande strålarna är vinkelräta mot projektionsplanet.
Hur kommer projektionen att förändras om det avbildade föremålet roteras, till exempel runt dess höjd - kant AD (Fig. 109, b)?
Vid vändning kommer skuggan att krympa på bredden (linjerna a’b’ och c’d’ i fig. 109, b blir kortare). Om vi fortsätter att rotera pappersarket, noterar vi att i en position vinkelrätt mot väggen kommer bilden av arket att förvandlas till en linje (fig. 109, c), men objektets höjd förblir konstant, dvs linjerna a' d' och b'c' längs längden är inte förvrängda.
Låt oss nu formulera slutsatser om vilken form och storlek bilder ett platt objekt har i rektangulära projektioner, olika placerade i förhållande till projektionsplanet:
a) en platt figur parallell med projektionsplanet är avbildad på den i naturlig storlek (fig. 109, a);
b) en platt figur, lutande mot projektionsplanet, är avbildad på den med en förvrängning av dimensioner (fig. 109, b);
c) en platt figur vinkelrät mot projektionsplanet är avbildad på den i form av ett rakt linjesegment (fig. 109, c).
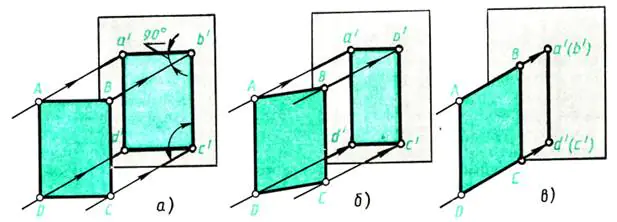
Ris. 109. Projicera en platt figur
Dessa fynd relaterar till skildringen av kanterna på föremål.
Hur avbildas kanterna på föremål, det vill säga linjer, i rektangulära projektioner?
Låt oss upprepa experimentet med att rotera ett plant föremål, observera hur dess kanter, d.v.s. linjer, projiceras och dra slutsatser:
a) ett rät linjesegment parallellt med projektionsplanet avbildas på det i naturlig storlek (jämför höjden på föremålet AD och BC i fig. 109, a, b, c med dess projektioner a'd' och b'c, och bredden på objektet AB och CD med dess utsprång a'b' och c'd' i fig. 109, a);
b) ett rakt segment som lutar mot projektionsplanet är avbildat på det med en förvrängning i längd (jämför bredden på objektet AB och CD i fig. 109, b med dess projektioner a'b' och c'd');
c) ett rakt linjesegment vinkelrätt mot projektionsplanet avbildas av en punkt på det (se i fig. 109, tvärs över objektets bredd - linjerna AB och CD, vinkelräta mot projektionsplanet).
Projektionen av en punkt är basen för en vinkelrät sänkt från en given punkt i rymden till projektionsplanet (se punkterna a', b', c', d' - projektioner av punkterna A, B, C, D).
Låt oss komma överens om att beteckna punkter i rymden med versaler A, B, C, D, etc., och projektioner av punkter med motsvarande gemener i, b, c, d, etc.
Av de två punkter som sammanfaller i ritningen (fig. 109, c) är den ena en bild av en synlig vertex, och den andra är en osynlig (sluten) en. Beteckningen på projektioner av osynliga hörn tas inom parentes.



