Sektioner: Teknologi
Mål og mål for lektionen:
pædagogisk: vise eleverne, hvordan man bruger den rektangulære projektionsmetode, når de laver en tegning;
• behovet for at bruge tre projektionsplaner;
• skabe betingelser for dannelse af færdigheder til at projicere et objekt på tre projektionsplaner;
udvikler: udvikle rumlige begreber, rumlig tænkning, kognitiv interesse og kreative evner hos eleverne;
uddanne: ansvarlig holdning til tegning, at dyrke en kultur for grafisk arbejde.
Metoder og teknikker til undervisning: forklaring, samtale, problemsituationer, research, øvelser, frontalt arbejde med klassen, kreativt arbejde.
Materialestøtte: computere, præsentation ”Rektangulær projektion”, opgaver, øvelser, øvelseskort, oplæg til selvtest.
Lektionstype: lektion for at konsolidere viden.
Ordforrådsarbejde: vandret plan, projektion, projektion, profil, research, projekt.
I. Organisatorisk del.
Angiv emnet og formålet med lektionen.
Lad os udføre lektion-konkurrence, for hver opgave vil du modtage et vist antal point. Afhængigt af de scorede point, vil der blive tildelt en karakter for lektionen.
II. Gentagelse af projektion og dens typer.
Projektion er den mentale proces med at konstruere billeder af objekter på et plan.
Gentagelse udføres ved hjælp af præsentation.
1. Eleverne bliver spurgt problematisk situation. (Præsentation 1)
Analyser den geometriske form af delen på frontprojektionen og find denne del blandt de visuelle billeder.

Ud fra denne situation konkluderes det, at alle 6 dele har samme frontale projektion. Det betyder, at én projektion ikke altid giver et fuldstændigt billede af delens form og design.
- Hvad er vejen ud af denne situation? (Se på delen fra den anden side).
2. Der var behov for at bruge et andet projektionsplan. (Horisontal projektion).
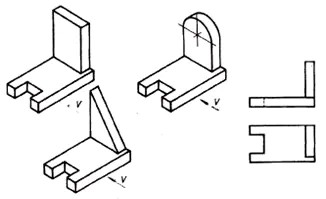
3. Behovet for en tredje projektion opstår, når to projektioner ikke er nok til at bestemme formen på et objekt.
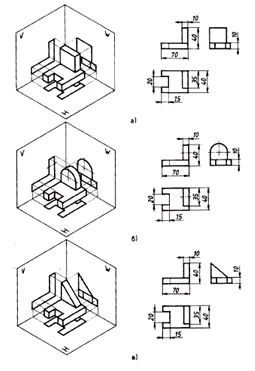
Størrelse:
- på frontal projektion –
Konklusion: det betyder, at for at lære at lave tegninger, skal du være i stand til at projicere objekter på et plan.
Udfyld de manglende ord i definitionsteksten.
1. Der er _______________ og ______________ projektion.
2. Hvis der kommer ______________ stråler ud fra et punkt, kaldes projektion ______________.
3. Hvis ______________ stråler er rettet parallelt, kaldes projektion ____________.
4. Hvis ______________ stråler er rettet parallelt med hinanden og i en vinkel på 90 ° til projektionsplanet, så kaldes projektionen ______________.
5. Et naturligt billede af et objekt på et projektionsplan opnås kun med ______________ projektion.
6. Fremspringene er placeret i forhold til hinanden______________________________.
7. Grundlæggeren af den rektangulære projektionsmetode er _______________
Opgave 2. Forskningsprojekt
Match hovedtyperne angivet med tal med delene angivet med bogstaver, og skriv svaret i din notesbog.
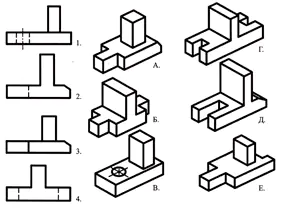
En øvelse til at gennemgå viden om geometriske legemer.
Brug den verbale beskrivelse til at finde et visuelt billede af delen.
Basen af delen har form af et rektangulært parallelepipedum, hvis mindre flader har riller i form af et regulært firkantet prisme. I midten af den øvre flade af parallelepipedet er der en afkortet kegle, langs hvis akse der er et gennemgående cylindrisk hul.
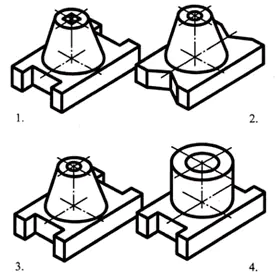
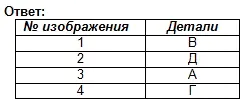
Svar: del nr. 3 (1 point)
Find overensstemmelsen mellem de tekniske tegninger af delene og deres frontale fremspring (projektionsretningen er markeret med en pil). Ud fra de spredte billeder af tegningen, lav en tegning af hver del, bestående af tre billeder. Skriv dit svar i tabellen (fig. 129).
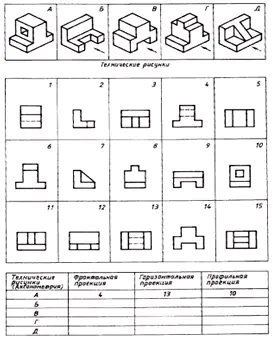
| Tekniske tegninger | Frontal projektion | Vandret projektion | Profilprojektion |
| EN | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| I | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktisk arbejde.
Opgave nr. 1. Forskningsprojekt
Find frontale og vandrette projektioner for dette visuelle billede. Skriv svaret i din notesbog.
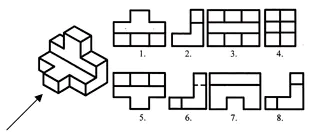
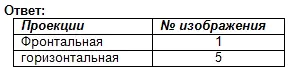
Vurdering af arbejdet i lektionen. Selv test. (Præsentation 2)
Pointene for karaktergivning af første del af arbejdet er skrevet på tavlen:
Opgave nr. 2. Kreativt arbejde og verifikation af dets implementering
(kreativt projekt)
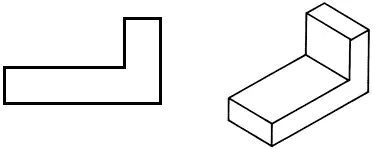
• Tegn den frontale projektion ind i din projektmappe.
• Tegn et vandret projektion, og ændre formen på delen for at reducere dens masse.
• Foretag om nødvendigt ændringer i frontalprojektionen.
• For at kontrollere færdiggørelsen af opgaven, kalder du en eller to elever til tavlen for at forklare deres løsning på problemet.
IV. Opsummering af lektionen.
1. Vurdering af arbejde i timen. (Tjekker den praktiske del af arbejdet)
V. Hjemmeopgave.
1. Forskningsprojekt.
Arbejd i henhold til tabellen: Bestem hvilken tegning, angivet med et tal, der svarer til tegningen, angivet med et bogstav.
Et særligt tilfælde af parallel projektion, hvor projektionsretningen er vinkelret på projektionsplanet, kaldes rektangulær eller ortogonal projektion. Den rektangulære (ortogonale) projektion af et punkt er bunden af den vinkelrette tegnet fra punktet til projektionsplanet. Den rektangulære projektion af punkterne A og B er vist i fig. 5.
For at bestemme positionen af et punkt i rummet ud fra dets parallelle projektioner er det nødvendigt at have to parallelle planer opnået i to projektionsretninger.
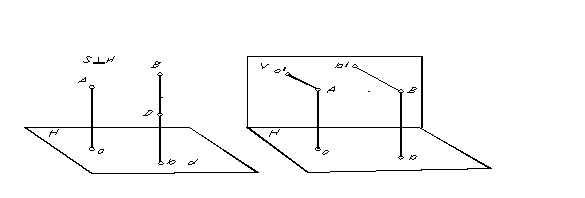 |
Fordi gennem et punkt kan der kun tegnes en ret linje vinkelret på planet, så med ortogonal projektion er det naturligvis nødvendigt at have to ikke-parallelle projektionsplaner for at opnå to projektioner af et punkt (fig. 6). .
Ortografisk projektion har en række fordele i forhold til central og parallel projektion. Disse omfatter primært:
1. Enkelhed af grafiske konstruktioner til bestemmelse af ortogonale projektioner af punkter.
2. Evnen til under visse betingelser at bevare formen og størrelsen af den projicerede figur på fremspring.
De bemærkede fordele har sikret den udbredte brug af ortogonal projektion i teknologi, især til udarbejdelse af maskintekniske tegninger.
I maskinteknik, for at være i stand til ud fra en tegning at bedømme formen og størrelsen af de afbildede genstande, når de tegner tegninger, bruger de som regel ikke to, men flere projektionsplaner.
Positionen af et punkt i rummet, og derfor af enhver geometrisk figur, kan bestemmes, hvis et hvilket som helst koordinatreferencesystem er specificeret. Projektionsplaner opdeler rummet i otte dele - oktanter. De er konventionelt nummereret med romertal (fig. 7).
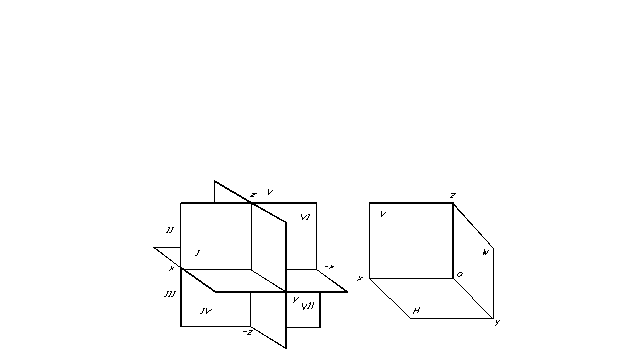
Projektionsplaner opdeler rummet i otte dele - oktanter. De er konventionelt nummereret med romertal (fig. 7).
Det mest bekvemme til at fiksere en geometrisk figurs position i rummet og identificere dens form fra ortogonale projektioner er det kartesiske koordinatsystem, der består af tre indbyrdes vinkelrette projektionsplaner. På grund af det faktum, at beskrivende geometri er designet til at formidle resultaterne af dens teoretiske forskning til praktisk brug, er det tilrådeligt at overveje ortogonal projektion også i et system med tre projektionsplaner.
For at lette projektionen er tre indbyrdes vinkelrette planer valgt som tre projektionsplaner (fig. 8). En af dem er normalt placeret vandret - det kaldes vandret projektionsplan, den anden er lodret, parallel med tegneplanet, kaldes det frontal plan af projektioner og en tredje, vinkelret på de to eksisterende - hedder det profilplan af projektioner. Disse projektionsplaner skærer langs linjer kaldet projektionsakser.
Vi har taget et højrehåndssystem til at arrangere projektionsplaner. I dette tilfælde betragtes de positive retninger af akserne: for aksen x (skæring af vandrette og frontale projektionsplaner) – til venstre for origo, for aksen y (skæring af vandrette og profilprojektionsplaner) – mod observatøren fra frontprojektionsplanet, for aksen z (skæring af frontale og profilplaner af projektioner) - opad fra det horisontale plan af projektioner betragtes de modsatte retninger af akserne som negative.
Projektionen af et punkt er bunden af den vinkelrette tegnet fra punktet til det tilsvarende projektionsplan. Vandret projektion punkter er den rektangulære projektion af et punkt på et vandret projektionsplan, frontal projektion – henholdsvis på det frontale plan af projektioner og profil – på projektionernes profilplan.
Det er ubelejligt at bruge dette rumlige layout til at afbilde ortogonale projektioner af geometriske figurer på grund af dets omfang, og også på grund af det faktum, at på individuelle (vandret og profil) formen og størrelsen af den projicerede figur er forvrænget. Derfor bruger de i stedet for at afbilde et rumligt layout i en tegning en kompleks tegning (Monge-diagram) sammensat af tre indbyrdes forbundne ortogonale projektioner af en geometrisk figur.
Transformationen af det rumlige layout til diagrammer udføres ved at kombinere horisontal- og profilprojektionsplanerne med frontprojektionsplanet (fig. 7).
Da planerne ikke har nogen grænser, er grænserne for planerne ikke vist i den kombinerede position (på diagrammet), er der ingen grund til at efterlade inskriptioner, der angiver projektionsplanernes position (fig. 10).
Efter at have skiftet til diagrammet gik den rumlige klarhed tabt. Diagrammet giver mere - nøjagtighed og nem måling af billeder, med enkel konstruktion. Men at forestille sig et rumligt billede kræver fantasiarbejde.
Fandt du ikke det, du ledte efter? Brug søgningen:
Bedste ordsprog: For en studerende er det vigtigste ikke at bestå eksamen, men at huske på det i tide. 9744 — | 7364 - eller læs alt.
Projektionstegning (grundlæggende om beskrivende geometri)
Fremskrivningsmetode
Rektangulær projektionsmetode
Hvis de fremspringende stråler danner en ret vinkel med projektionsplanet, kaldes sådanne projektioner rektangulær.
Rektangulære projektioner kaldes også ortogonal. Ordet "ortogonal" kommer fra de græske ord "ortos" - lige og "gonia" - vinkel.
Tegninger i systemet med rektangulære projektioner giver et komplet billede af objektets form og størrelse. De er lettere at udføre end aksonometriske projektioner.
Hvad skal du vide for at fuldføre tegninger?
Enhver genstand, der har flade overflader, er begrænset af spidser, kanter og flader (fig. 108). Derfor, for at lære at afbilde forskellige objekter i tegninger, skal du vide, hvordan hjørner (punkter), kanter (segmenter af lige linjer) og kanter af objekter (dele af et plan) er afbildet i rektangulære projektioner.
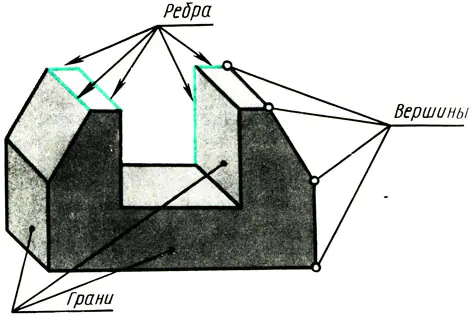
Ris. 108. Premsch som et sæt af punkter, skriv. Hjørnepunkter af fly
Lad os lave et simpelt eksperiment. Lad os se, hvordan en flad genstand og hundrede elementer er afbildet i forskellige positioner.
Lad os tage væggen modsat vinduet som projektionsplan. Lad det ud af vinduet vinkelret Lysstråler falder på væggen - projekterende stråler. Læg et ark tykt ABCD-papir foran væggen (parallelt med den) (fig. 109, a). Der dannes en skygge på væggen, svarende til objektets projektion. Hvad er dens dimensioner? I dette tilfælde svarer projektionen a'b'c'd' i form og størrelse til projektionsobjektet - arket
ABCD. Projektionsmetoden er rektangulær, da de projekterende stråler er vinkelrette på projektionsplanet.
Hvordan vil projektionen ændre sig, hvis det afbildede objekt for eksempel drejes rundt om dets højde - kant AD (fig. 109, b)?
Når man drejer, vil skyggen krympe i bredden (linierne a’b’ og c’d’ i fig. 109, b bliver kortere). Hvis vi fortsætter med at rotere papirarket, bemærker vi, at i en position vinkelret på væggen vil billedet af arket blive til en linje (fig. 109, c), men objektets højde forbliver konstant, dvs. linjerne a' d' og b'c' langs længden er ikke forvrænget.
Lad os nu formulere konklusioner om, hvilken form og størrelse billeder et fladt objekt har i rektangulære projektioner, forskelligt placeret i forhold til projektionsplanet:
a) en flad figur parallelt med projektionsplanet er afbildet på den i naturlig størrelse (fig. 109, a);
b) en flad figur, der skråner til projektionsplanet, er afbildet på den med en forvrængning af dimensioner (fig. 109, b);
c) en flad figur vinkelret på projektionsplanet er afbildet på den i form af et lige linjesegment (fig. 109, c).
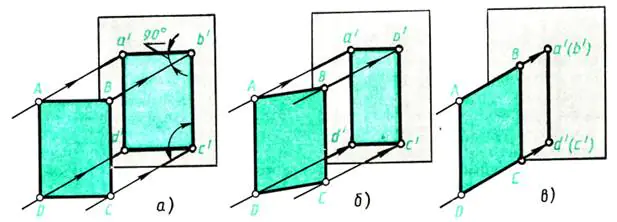
Ris. 109. Projicering af en flad figur
Disse fund vedrører afbildningen af kanterne på objekter.
Hvordan er kanterne på objekter, dvs. linjer, afbildet i rektangulære projektioner?
Lad os gentage eksperimentet med at rotere et fladt objekt, observere, hvordan dets kanter, dvs. linjer, projiceres, og drage konklusioner:
a) et lige linjestykke parallelt med projektionsplanet er afbildet på det i naturlig størrelse (sammenlign højden af objektet AD og BC i fig. 109, a, b, c med dets projektioner a'd' og b'c, og bredden af objektet AB og CD med dets fremspring a'b' og c'd' i fig. 109, a);
b) et lige segment, der hælder til projektionsplanet, er afbildet på det med en forvrængning i længden (sammenlign bredden af objektet AB og CD i fig. 109, b med dets fremspring a'b' og c'd');
c) et lige linjesegment vinkelret på projektionsplanet er afbildet af et punkt på det (se i fig. 109, på tværs af objektets bredde - linjerne AB og CD, vinkelret på projektionsplanet).
Projektionen af et punkt er bunden af en vinkelret sænket fra et givet punkt i rummet til projektionsplanet (se punkterne a', b', c', d' - projektioner af punkterne A, B, C, D).
Lad os blive enige om at betegne punkter i rummet med store bogstaver A, B, C, D osv., og projektioner af punkter med de tilsvarende små bogstaver i, b, c, d osv.
Af de to punkter, der falder sammen på tegningen (fig. 109, c), er det ene et billede af et synligt toppunkt, og det andet er et usynligt (lukket). Udpegningen af projektioner af usynlige hjørner er taget i parentes.



