Secciones: Tecnología
Metas y objetivos de la lección:
educativo: mostrar a los estudiantes cómo utilizar el método de proyección rectangular al hacer un dibujo;
• la necesidad de utilizar tres planos de proyección;
• crear condiciones para la formación de habilidades para proyectar un objeto en tres planos de proyección;
desarrollando: desarrollar conceptos espaciales, pensamiento espacial, interés cognitivo y habilidades creativas de los estudiantes;
educando: Actitud responsable ante el dibujo, cultivar una cultura del trabajo gráfico.
Métodos y técnicas de enseñanza: explicación, conversación, situaciones problemáticas, investigación, ejercicios, trabajo frontal con la clase, trabajo creativo.
Material de soporte: ordenadores, presentación “Proyección rectangular”, tareas, ejercicios, fichas de ejercicios, presentación para autoevaluación.
Tipo de lección: lección para consolidar conocimientos.
Trabajo de vocabulario: plano horizontal, proyección, proyección, perfil, investigación, proyecto.
I. Parte organizativa.
Indique el tema y el propósito de la lección.
llevemos a cabo competencia de lecciones, por cada tarea recibirás una cierta cantidad de puntos. Dependiendo de los puntos obtenidos, se asignará una calificación para la lección.
II. Revisión de proyección y sus tipos.
La proyección es el proceso mental de construir imágenes de objetos en un plano.
La repetición se realiza mediante presentación.
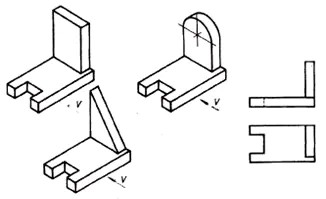
1. Se pregunta a los estudiantes situación problemática. (Presentación 1)
Analice la forma geométrica de la pieza en la proyección frontal y encuentre esta pieza entre las imágenes visuales.

De esta situación se concluye que las 6 partes tienen la misma proyección frontal. Esto significa que una proyección no siempre da una imagen completa de la forma y el diseño de la pieza.
- ¿Cuál es la salida a esta situación? (Mira la pieza desde el otro lado).
2. Era necesario utilizar otro plano de proyección. (Proyección horizontal).
3. La necesidad de una tercera proyección surge cuando dos proyecciones no son suficientes para determinar la forma de un objeto.
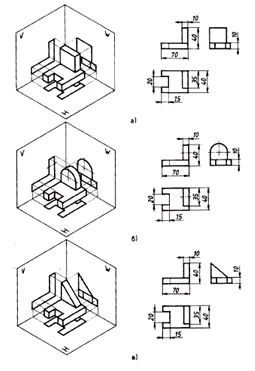
Dimensionamiento:
- en la proyección frontal –
Conclusión: esto significa que para aprender a hacer dibujos es necesario poder proyectar objetos en un plano.
Complete las palabras que faltan en el texto de definición.
1. Hay _______________ y ______________ proyección.
2. Si de un punto salen ______________ rayos, la proyección se llama ______________.
3. Si ______________ rayos se dirigen paralelos, la proyección se llama _____________.
4. Si los rayos ______________ se dirigen paralelos entre sí y en un ángulo de 90 ° con respecto al plano de proyección, entonces la proyección se llama ______________.
5. Una imagen natural de un objeto en un plano de proyección se obtiene sólo con proyección ______________.
6. Las proyecciones están ubicadas entre sí______________________________.
7. El fundador del método de proyección rectangular es _______________
Tarea 2. Proyecto de investigación
Une los tipos principales indicados por números con las partes indicadas por letras y escribe la respuesta en tu cuaderno.
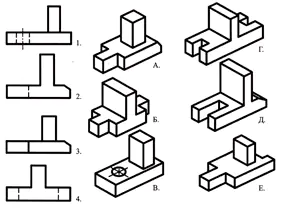
Un ejercicio de repaso de conocimientos sobre cuerpos geométricos.
Usando la descripción verbal, encuentre una imagen visual de la pieza.
La base de la pieza tiene forma de paralelepípedo rectangular, cuyas caras menores presentan ranuras en forma de prisma cuadrangular regular. En el centro de la cara superior del paralelepípedo hay un cono truncado, a lo largo de cuyo eje hay un agujero cilíndrico pasante.
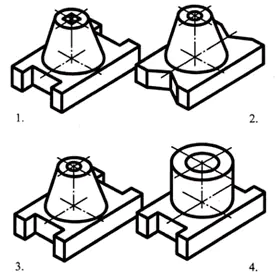
Respuesta: parte No. 3 (1 punto)
Encuentre la correspondencia entre los dibujos técnicos de las piezas y sus proyecciones frontales (la dirección de proyección está marcada con una flecha). A partir de las imágenes dispersas del dibujo, haz un dibujo de cada parte, que consta de tres imágenes. Escriba su respuesta en la tabla (Fig. 129).
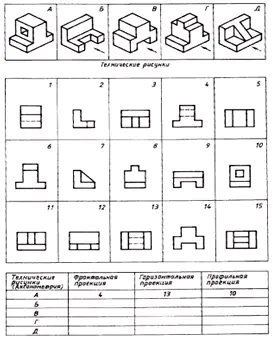
| Dibujos tecnicos | proyección frontal | Proyección horizontal | Proyección de perfil |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| EN | 14 | 5 | 1 |
| GRAMO | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Trabajo practico.
Tarea número 1. Proyecto de investigación
Encuentre las proyecciones frontal y horizontal de esta imagen visual. Escribe la respuesta en tu cuaderno.
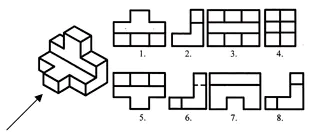
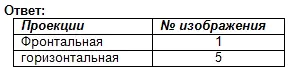
Evaluación del trabajo en la lección. Autotest. (Presentación 2)
Los puntos para calificar la primera parte del trabajo están escritos en la pizarra:
Tarea número 2. Trabajo creativo y verificación de su implementación.
(proyecto creativo)
• Dibuja la proyección frontal en tu libro de trabajo.
• Dibujar una proyección horizontal, cambiando la forma de la pieza para reducir su masa.
• Si es necesario, realice cambios en la proyección frontal.
• Para comprobar la finalización de la tarea, llame a uno o dos estudiantes a la pizarra para que expliquen su solución al problema.
IV. Resumiendo la lección.
1. Evaluación del trabajo en la lección. (Comprobando la parte práctica del trabajo)
V. Asignación de tareas.
1. Proyecto de investigación.
Trabajar según la tabla: determinar qué dibujo, designado por un número, corresponde al dibujo, designado por una letra.
Un caso especial de proyección paralela, en el que la dirección de proyección es perpendicular al plano de proyección, se llama rectangular o proyección ortogonal. La proyección rectangular (ortogonal) de un punto es la base de la perpendicular trazada desde el punto al plano de proyección. La proyección rectangular de los puntos A y B se muestra en la Fig. 5.
Para determinar la posición de un punto en el espacio a partir de sus proyecciones paralelas, es necesario disponer de dos planos paralelos obtenidos en dos direcciones de proyección.
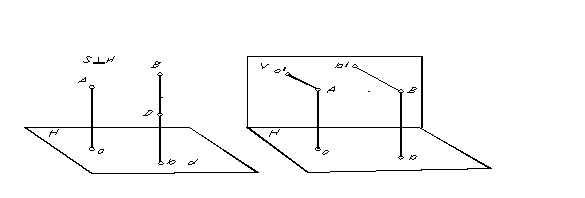 |
Porque a través de un punto solo se puede trazar una recta perpendicular al plano, entonces, obviamente, con proyección ortogonal, para obtener dos proyecciones de un punto es necesario tener dos planos de proyección no paralelos (Fig.6) .
La proyección ortográfica tiene una serie de ventajas sobre la proyección central y paralela. Estos incluyen principalmente:
1. Sencillez de construcciones gráficas para determinar proyecciones ortogonales de puntos.
2. La capacidad, bajo determinadas condiciones, de conservar la forma y el tamaño de la figura proyectada en las proyecciones.
Las ventajas observadas garantizaron el uso generalizado de la proyección ortogonal en tecnología, en particular, para la preparación de dibujos de ingeniería mecánica.
En la ingeniería mecánica, para poder juzgar a partir de un dibujo la forma y el tamaño de los objetos representados, en la elaboración de los dibujos se utilizan, por regla general, no dos, sino varios planos de proyección.
La posición de un punto en el espacio, y por tanto de cualquier figura geométrica, se puede determinar si se especifica cualquier sistema de referencia de coordenadas. Los planos de proyección dividen el espacio en ocho partes: octantes. Están numerados convencionalmente con números romanos (Fig. 7).
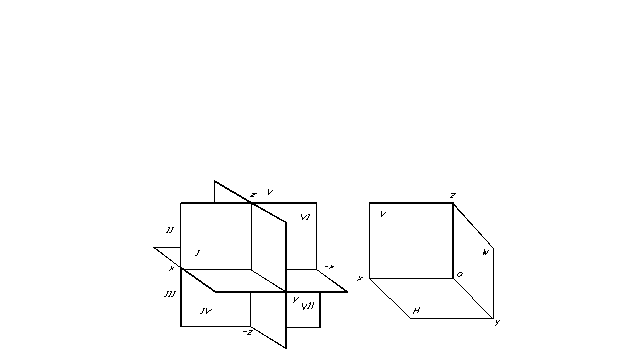
Los planos de proyección dividen el espacio en ocho partes: octantes. Están numerados convencionalmente con números romanos (Fig. 7).
El más conveniente para fijar la posición de una figura geométrica en el espacio e identificar su forma a partir de proyecciones ortogonales es el sistema de coordenadas cartesiano, que consta de tres planos de proyección mutuamente perpendiculares. Debido a que la geometría descriptiva está diseñada para transmitir los resultados de su investigación teórica para un uso práctico, es aconsejable considerar la proyección ortogonal también en un sistema de tres planos de proyección.
Para facilitar la proyección, se eligen tres planos mutuamente perpendiculares como tres planos de proyección (Fig. 8). Uno de ellos generalmente se coloca horizontalmente; se llama plano de proyección horizontal, el otro es vertical, paralelo al plano del dibujo, se llama plano frontal de proyecciones y un tercero, perpendicular a los dos existentes -se llama Plano de perfil de proyecciones. Estos planos de proyección se cruzan a lo largo de líneas llamadas ejes de proyección.
Hemos adoptado un sistema diestro para organizar los planos de proyección. En este caso se consideran los sentidos positivos de los ejes: para el eje X (intersección de los planos de proyección horizontal y frontal) – a la izquierda del origen, para el eje y (intersección de los planos de proyección horizontal y de perfil) – hacia el observador desde el plano de proyección frontal, para el eje z (intersección de los planos de proyección frontal y de perfil): hacia arriba desde el plano horizontal de proyección, las direcciones opuestas de los ejes se consideran negativas.
La proyección de un punto es la base de la perpendicular trazada desde el punto sobre el plano de proyección correspondiente. Proyección horizontal los puntos son la proyección rectangular de un punto en un plano de proyección horizontal, proyección frontal – respectivamente en el plano frontal de proyecciones y perfil - en el plano del perfil de proyecciones.
Es inconveniente utilizar esta disposición espacial para representar proyecciones ortogonales de figuras geométricas debido a su volumen, así como al hecho de que en las individuales (horizontales y de perfil) la forma y el tamaño de la figura proyectada están distorsionados. Por lo tanto, en lugar de representar una distribución espacial en un dibujo, utilizan un dibujo complejo (diagrama de Monge) compuesto por tres proyecciones ortogonales interconectadas de una figura geométrica.
La transformación de la distribución espacial en diagramas se realiza combinando los planos de proyección horizontal y de perfil con el plano de proyección frontal (Fig. 7).
Dado que los planos no tienen límites, en la posición combinada (en el diagrama) no se muestran los límites de los planos, no es necesario dejar inscripciones que indiquen la posición de los planos de proyección (Fig. 10).
Al cambiar al diagrama, se perdió la claridad espacial. El diagrama ofrece más precisión y facilidad de medición de imágenes, con simplicidad de construcción. Sin embargo, imaginar una imagen espacial requiere el trabajo de la imaginación.
¿No encontraste lo que buscabas? Utilice la búsqueda:
Mejores dichos: Para un estudiante, lo más importante no es aprobar el examen, sino recordarlo a tiempo. 9744 — | 7364 - o leer todo.
Dibujo de proyección (conceptos básicos de geometría descriptiva)
Método de proyección
Método de proyección rectangular
Si los rayos proyectados forman un ángulo recto con el plano de proyección, entonces tales proyecciones se llaman rectangular.
Las proyecciones rectangulares también se llaman ortogonal. La palabra "ortogonal" proviene de las palabras griegas "ortos" - recto y "gonia" - ángulo.
Los dibujos en el sistema de proyecciones rectangulares dan una imagen completa de la forma y el tamaño del objeto. Son más fáciles de realizar que las proyecciones axonométricas.
¿Qué necesitas saber para completar dibujos con éxito?
Cualquier objeto que tenga superficies planas está limitado por vértices, aristas y caras (Fig. 108). Por lo tanto, para aprender a representar varios objetos en dibujos, necesita saber cómo se representan los vértices (puntos), las aristas (segmentos de líneas rectas) y las aristas de los objetos (partes de un plano) en proyecciones rectangulares.
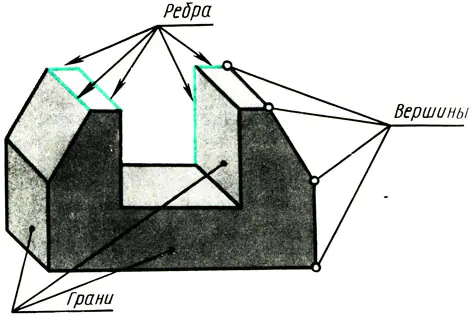
Arroz. 108. Premsch como conjunto de puntos, escribe. Vértices de planos
Hagamos un experimento sencillo. Veamos cómo se representan un objeto plano y cien elementos en diferentes posiciones.
Tomemos como plano de proyección la pared opuesta a la ventana. Déjalo salir por la ventana perpendicular Los rayos de luz caen sobre la pared, proyectando rayos. Coloque una hoja de papel ABCD grueso frente a la pared (paralela a ella) (Fig. 109, a). Se forma una sombra en la pared, equivalente a la proyección del objeto. ¿Cuales son sus dimensiones? En este caso, la proyección a’b’c’d’ corresponde en forma y tamaño al objeto de proyección: la hoja.
A B C D. El método de proyección es rectangular, ya que los rayos proyectados son perpendiculares al plano de proyección.
¿Cómo cambiará la proyección si el objeto representado se gira, por ejemplo, alrededor de su altura - borde AD (Fig. 109, b)?
Al girar, la sombra se reducirá en ancho (las líneas a'b' y c'd' en la Fig. 109, b se acortan). Continuando girando la hoja de papel, notamos que en una posición perpendicular a la pared, la imagen de la hoja se convertirá en una línea (Fig.109, c), pero la altura del objeto permanece constante, es decir, líneas a' d' y b'c' a lo largo no están distorsionados.
Ahora formulemos conclusiones sobre la forma y el tamaño de las imágenes que tiene un objeto plano en proyecciones rectangulares, ubicadas de manera diferente en relación con el plano de proyección:
a) en él se representa una figura plana paralela al plano de proyección en tamaño natural (Fig. 109, a);
b) en él se representa una figura plana, inclinada hacia el plano de proyección, con una distorsión de las dimensiones (Fig. 109, b);
c) en él se representa una figura plana perpendicular al plano de proyección en forma de segmento de línea recta (Fig. 109, c).
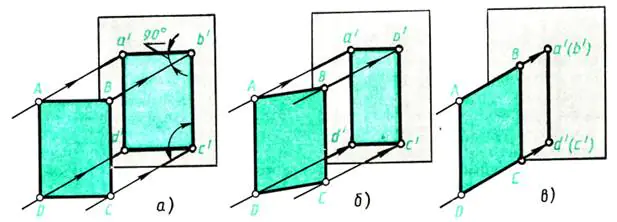
Arroz. 109. Proyectando una figura plana
Estos hallazgos se relacionan con la representación de los bordes de los objetos.
¿Cómo se representan los bordes de los objetos, es decir, las líneas, en proyecciones rectangulares?
Repitamos el experimento de girar un objeto plano, observemos cómo se proyectan sus bordes, es decir, sus líneas, y saquemos conclusiones:
a) en él se representa un segmento de línea recta paralelo al plano de proyección en tamaño natural (compare la altura del objeto AD y BC en la Fig. 109, a, b, c con sus proyecciones a'd' y b'c, y el ancho del objeto AB y CD con sus proyecciones a'b' y c'd' en la Fig. 109, a);
b) en él se representa un segmento recto inclinado al plano de proyección con una distorsión en longitud (compárese el ancho del objeto AB y CD en la Fig. 109, b con sus proyecciones a'b' y c'd');
c) un segmento de línea recta perpendicular al plano de proyección se representa mediante un punto (ver en la Fig. 109, a lo ancho del objeto: líneas AB y CD, perpendiculares al plano de proyección).
La proyección de un punto es la base de una perpendicular que desciende desde un punto dado en el espacio al plano de proyección (ver puntos a’, b’, c’, d’ - proyecciones de los puntos A, B, C, D).
Acordemos denotar puntos en el espacio con letras mayúsculas A, B, C, D, etc., y proyecciones de puntos con las correspondientes letras minúsculas i, b, c, d, etc.
De los dos puntos que coinciden en el dibujo (Fig. 109, c), uno es la imagen de un vértice visible y el otro es invisible (cerrado). La designación de proyecciones de vértices invisibles se toma entre paréntesis.



