Sekcje: Technologia
Cele i zadania lekcji:
edukacyjny: pokazać uczniom, jak wykorzystać metodę rzutu prostokątnego podczas wykonywania rysunku;
• potrzeba użycia trzech płaszczyzn projekcyjnych;
• stworzyć warunki do kształtowania umiejętności rzutowania obiektu na trzy płaszczyzny projekcyjne;
rozwijanie: rozwijać koncepcje przestrzenne, myślenie przestrzenne, zainteresowania poznawcze i zdolności twórcze uczniów;
kształcenie: odpowiedzialne podejście do rysunku, kultywowanie kultury pracy graficznej.
Metody i techniki nauczania: wyjaśnianie, rozmowa, sytuacje problemowe, badania, ćwiczenia, praca frontalna z klasą, praca twórcza.
Wsparcie merytoryczne: komputery, prezentacja „Projekt prostokątny”, zadania, ćwiczenia, karty ćwiczeń, prezentacja do samodzielnego sprawdzenia.
Rodzaj lekcji: lekcja utrwalająca wiedzę.
Praca słownictwa: płaszczyzna pozioma, projekcja, projekcja, profil, badania, projekt.
I. Część organizacyjna.
Podaj temat i cel lekcji.
Przeprowadźmy lekcja-konkurs, za każde zadanie otrzymasz określoną liczbę punktów. W zależności od zdobytych punktów zostanie przypisana ocena za lekcję.
II. Powtórzenie projekcji i jej rodzaje.
Projekcja to mentalny proces konstruowania obrazów obiektów na płaszczyźnie.
Powtórzenie odbywa się za pomocą prezentacji.
1. Studenci są proszeni problematyczna sytuacja. (Prezentacja 1)
Przeanalizuj kształt geometryczny części na projekcji przedniej i znajdź tę część wśród obrazów wizualnych.

Z tej sytuacji wnioskuje się, że wszystkie 6 części ma taki sam występ przedni. Oznacza to, że jeden rzut nie zawsze daje pełny obraz kształtu i konstrukcji części.
- Jakie jest wyjście z tej sytuacji? (Spójrz na część z drugiej strony).
2. Zaistniała konieczność wykorzystania innej płaszczyzny projekcyjnej. (Rzut poziomy).
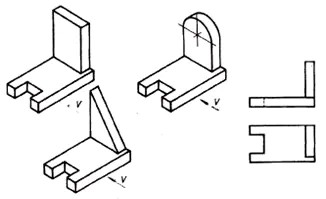
3. Potrzeba trzeciego rzutu powstaje, gdy dwa rzuty nie wystarczą do określenia kształtu przedmiotu.
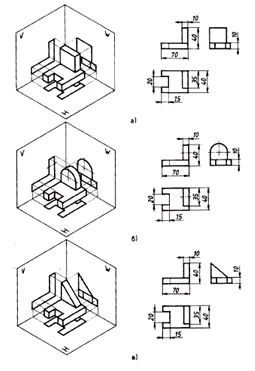
Rozmiar:
- na projekcji czołowej –
Wniosek: oznacza to, że aby nauczyć się rysować, musisz umieć rzutować obiekty na płaszczyznę.
Uzupełnij brakujące słowa w tekście definicji.
1. Istnieją projekcje ______________ i _____________.
2. Jeżeli z jednego punktu wychodzi ______________ promieni, projekcja nazywa się ______________.
3. Jeśli ______________ promienie są skierowane równolegle, projekcja nazywa się _____________.
4. Jeżeli promienie ______________ są skierowane równolegle do siebie i pod kątem 90 ° do płaszczyzny projekcji, wówczas rzut nazywa się ______________.
5. Naturalny obraz obiektu na płaszczyźnie projekcji uzyskuje się tylko przy projekcji ______________.
6. Występy są umieszczone względem siebie______________________________.
7. Twórcą metody rzutowania prostokątnego jest ______________
Zadanie 2. Projekt badawczy
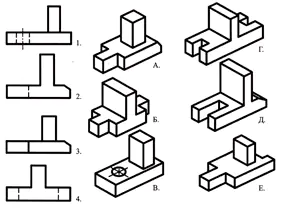
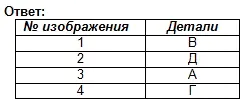
Dopasuj główne typy oznaczone cyframi do części oznaczonych literami i zapisz odpowiedź w zeszycie.
Ćwiczenie sprawdzające wiedzę o ciałach geometrycznych.
Korzystając z opisu słownego, znajdź wizualny obraz części.
Podstawa części ma kształt prostokątnego równoległościanu, którego mniejsze ściany posiadają rowki w kształcie regularnego czworokątnego pryzmatu. Pośrodku górnej powierzchni równoległościanu znajduje się ścięty stożek, wzdłuż którego osi znajduje się przelotowy cylindryczny otwór.
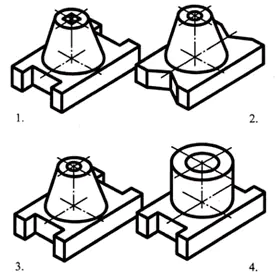
Odpowiedź: część nr 3 (1 punkt)
Znajdź zgodność pomiędzy rysunkami technicznymi części a ich rzutami czołowymi (kierunek rzutowania zaznaczony jest strzałką). Na podstawie rozproszonych obrazów rysunku wykonaj rysunek każdej części, składający się z trzech obrazów. Zapisz odpowiedź w tabeli (ryc. 129).
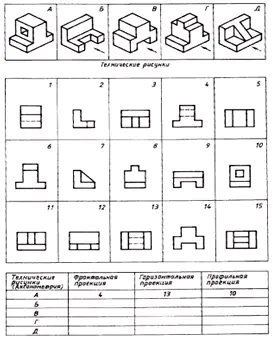
| Rysunki techniczne | Projekcja czołowa | Rzut poziomy | Projekcja profilu |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| W | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktyczna praca.
Zadanie nr 1. Projekt badawczy
Znajdź rzuty czołowe i poziome tego obrazu. Zapisz odpowiedź w zeszycie.
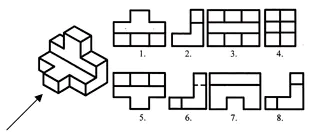
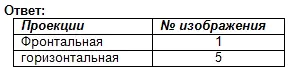
Ocena pracy na lekcji. Autotest. (Prezentacja 2)
Punkty za ocenę pierwszej części pracy wypisane są na tablicy:
Zadanie nr 2. Praca twórcza i weryfikacja jej realizacji
(projekt kreatywny)
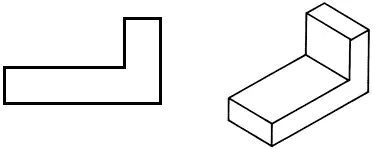
• Narysuj projekcję czołową w swoim zeszycie.
• Narysuj rzut poziomy, zmieniając kształt części w celu zmniejszenia jej masy.
• Jeśli to konieczne, dokonaj zmian w projekcji czołowej.
• Aby sprawdzić wykonanie zadania, zawołaj jednego lub dwóch uczniów do tablicy, aby wyjaśnili swoje rozwiązanie problemu.
IV. Podsumowanie lekcji.
1. Ocena pracy na lekcji. (Sprawdzanie części praktycznej pracy)
V. Zadanie domowe.
1. Projekt badawczy.
Pracuj zgodnie z tabelą: określ, który rysunek oznaczony liczbą odpowiada rysunkowi oznaczonemu literą.
Nazywa się szczególny przypadek rzutowania równoległego, w którym kierunek rzutu jest prostopadły do płaszczyzny rzutowania prostokątny Lub rzut ortogonalny. Rzut prostokątny (ortogonalny) punktu jest podstawą prostopadłej poprowadzonej z punktu na płaszczyznę rzutowania. Rzut prostokątny punktów A i B pokazano na ryc. 5.
Aby określić położenie punktu w przestrzeni na podstawie jego równoległych rzutów, konieczne jest uzyskanie dwóch równoległych płaszczyzn w dwóch kierunkach rzutowania.
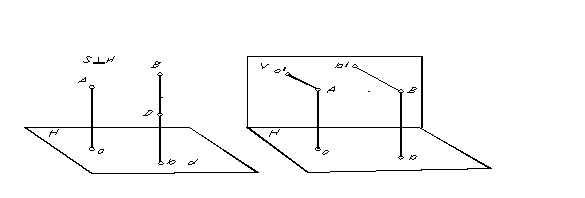 |
Ponieważ przez punkt można poprowadzić tylko jedną prostą prostopadłą do płaszczyzny, wówczas oczywiście przy rzucie ortogonalnym, aby uzyskać dwa rzuty jednego punktu, konieczne są dwie nierównoległe płaszczyzny rzutowania (rys. 6) .
Rzut ortograficzny ma wiele zalet w porównaniu z rzutowaniem centralnym i równoległym. Należą do nich przede wszystkim:
1. Prostota konstrukcji graficznych do wyznaczania rzutów ortogonalnych punktów.
2. Zdolność, pod pewnymi warunkami, do zachowania kształtu i wielkości rzutowanej figury na projekcjach.
Wskazane zalety zapewniły szerokie zastosowanie rzutowania ortogonalnego w technologii, w szczególności przy sporządzaniu rysunków technicznych.
W inżynierii mechanicznej, aby móc ocenić na podstawie rysunku kształt i rozmiar przedstawionych obiektów, przy sporządzaniu rysunków z reguły używają nie dwóch, ale kilku płaszczyzn projekcji.
Położenie punktu w przestrzeni, a tym samym dowolnej figury geometrycznej, można określić, jeśli zostanie określony dowolny układ odniesienia za pomocą współrzędnych. Płaszczyzny projekcyjne dzielą przestrzeń na osiem części - oktanty. Numerowane są umownie cyframi rzymskimi (ryc. 7).
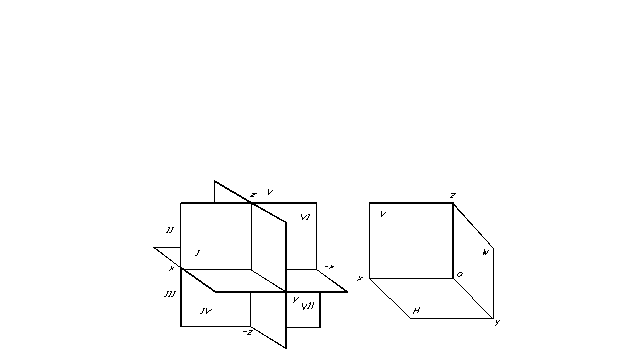
Płaszczyzny projekcyjne dzielą przestrzeń na osiem części - oktanty. Numerowane są umownie cyframi rzymskimi (ryc. 7).
Najwygodniejszym do ustalenia położenia figury geometrycznej w przestrzeni i identyfikacji jej kształtu na podstawie rzutów ortogonalnych jest kartezjański układ współrzędnych, składający się z trzech wzajemnie prostopadłych płaszczyzn rzutowania. Z uwagi na to, że geometria wykreślna ma na celu przekazanie wyników swoich badań teoretycznych do zastosowań praktycznych, wskazane jest uwzględnienie rzutowania ortogonalnego także w układzie trzech płaszczyzn rzutowania.
Dla ułatwienia projekcji jako trzy płaszczyzny projekcji wybiera się trzy wzajemnie prostopadłe płaszczyzny (ryc. 8). Jeden z nich jest zwykle umieszczony poziomo - tzw pozioma płaszczyzna projekcji, drugi jest pionowy, równoległy do płaszczyzny rysunku, tak się nazywa czołowa płaszczyzna występów i trzeci, prostopadły do dwóch istniejących - tzw płaszczyzna profilu występów. Te płaszczyzny projekcyjne przecinają się wzdłuż linii zwanych osie projekcji.
Przyjęliśmy prawoskrętny system ułożenia płaszczyzn projekcyjnych. W tym przypadku uwzględniane są dodatnie kierunki osi: dla osi X (przecięcie płaszczyzn rzutu poziomego i czołowego) – na lewo od początku układu współrzędnych, dla osi y (przecięcie płaszczyzny rzutowania poziomego i profilowego) – w stronę obserwatora z płaszczyzny rzutu czołowego, dla osi z (przecięcie płaszczyzny czołowej i profilowej rzutów) – w górę od poziomej płaszczyzny rzutów, przeciwne kierunki osi uważa się za ujemne.
Rzut punktu jest podstawą prostopadłej poprowadzonej z punktu na odpowiednią płaszczyznę rzutowania. Rzut poziomy punkty są prostokątnym rzutem punktu na poziomą płaszczyznę rzutowania, projekcja czołowa – odpowiednio na płaszczyźnie czołowej występów i profil – na płaszczyźnie profilu występów.
Wykorzystywanie tego układu przestrzennego do przedstawiania rzutów ortogonalnych figur geometrycznych jest niewygodne ze względu na jego masywność, a także ze względu na fakt, że na poszczególnych (poziomych i profilowych) kształt i wielkość rzutowanej figury są zniekształcone. Zamiast więc przedstawiać na rysunku układ przestrzenny, posługują się złożonym rysunkiem (diagram Monge'a) złożonym z trzech połączonych ze sobą ortogonalnych rzutów figury geometrycznej.
Przekształcenie układu przestrzennego na diagramy odbywa się poprzez połączenie płaszczyzny rzutowania poziomego i profilowego z płaszczyzną rzutu czołowego (ryc. 7).
Ponieważ płaszczyzny nie mają granic, w położeniu połączonym (na schemacie) granice płaszczyzn nie są pokazane, nie ma potrzeby pozostawiania napisów wskazujących położenie płaszczyzn rzutowania (ryc. 10).
Po przejściu na diagram utracono przejrzystość przestrzenną. Diagram daje więcej - dokładność i łatwość pomiaru obrazów, przy prostocie konstrukcji. Jednak wyobrażenie sobie obrazu przestrzennego wymaga pracy wyobraźni.
Nie znalazłeś tego, czego szukałeś? Skorzystaj z wyszukiwania:
Najlepsze powiedzenia: Dla studenta najważniejsze jest nie zdanie egzaminu, ale zawczasu o nim pamiętanie. 9744 — | 7364 - lub przeczytaj całość.
Rysunek rzutowy (podstawy geometrii wykreślnej)
Metoda projekcji
Metoda rzutowania prostokątnego
Jeśli wystające promienie tworzą kąt prosty z płaszczyzną projekcji, wówczas takie rzuty nazywane są prostokątny.
Prostokątne występy są również nazywane prostokątny. Słowo „ortogonalny” pochodzi od greckich słów „ortos” – prosty i „gonia” – kąt.
Rysunki w systemie rzutów prostokątnych dają pełny obraz kształtu i wielkości obiektu. Są łatwiejsze do wykonania niż rzuty aksonometryczne.
Co musisz wiedzieć, aby pomyślnie wykonać rysunki?
Każdy obiekt posiadający płaskie powierzchnie jest ograniczony wierzchołkami, krawędziami i ścianami (ryc. 108). Dlatego, aby nauczyć się przedstawiać różne obiekty na rysunkach, musisz wiedzieć, jak wierzchołki (punkty), krawędzie (odcinki linii prostych) i krawędzie obiektów (części płaszczyzny) są przedstawiane w rzutach prostokątnych.
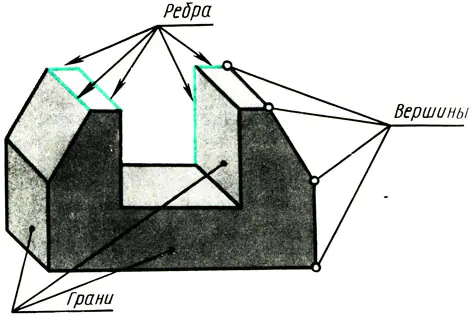
Ryż. 108. Premsch jako zbiór punktów napisz. Wierzchołki płaszczyzn
Zróbmy prosty eksperyment. Zobaczmy, jak płaski obiekt i sto elementów są przedstawione w różnych pozycjach.
Za płaszczyznę projekcyjną przyjmijmy ścianę naprzeciw okna. Wypuść to przez okno prostopadły Promienie światła padają na ścianę - rzucając promienie. Umieść arkusz grubego papieru ABCD przed ścianą (równolegle do niej) (ryc. 109, a). Na ścianie powstaje cień odpowiadający rzutowi obiektu. Jakie są jego wymiary? W tym przypadku występ a’b’c’d odpowiada kształtem i rozmiarem obiektowi projekcji – arkuszowi
ABCD. Metoda projekcji jest prostokątna, ponieważ promienie wystające są prostopadłe do płaszczyzny projekcji.
Jak zmieni się projekcja, jeśli przedstawiony obiekt zostanie obrócony np. wokół jego wysokości - krawędzi AD (ryc. 109, b)?
Podczas obracania cień zmniejszy się (linie a’b’ i c’d’ na ryc. 109, b staną się krótsze). Kontynuując obracanie kartki papieru, zauważamy, że w pozycji prostopadłej do ściany obraz arkusza zamieni się w linię (ryc. 109, c), ale wysokość obiektu pozostaje stała, tj. linie a' d' i b'c' wzdłuż długości nie są zniekształcone.
Sformułujmy teraz wnioski na temat tego, jaki kształt i rozmiar mają obrazy płaskiego obiektu w rzutach prostokątnych, różnie położonych w stosunku do płaszczyzny projekcji:
a) płaska figura równoległa do płaszczyzny projekcji jest na niej przedstawiona w naturalnym rozmiarze (ryc. 109, a);
b) przedstawiono na niej płaską figurę, nachyloną do płaszczyzny projekcji ze zniekształceniem wymiarów (ryc. 109, b);
c) przedstawiono na niej płaską figurę prostopadłą do płaszczyzny projekcji w postaci odcinka linii prostej (ryc. 109, c).
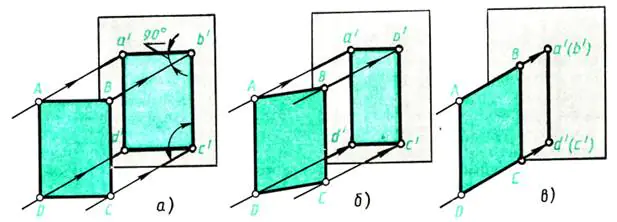
Ryż. 109. Rzutowanie płaskiej sylwetki
Ustalenia te dotyczą przedstawienia krawędzi obiektów.
Jak krawędzie obiektów, czyli linie, są przedstawiane w rzutach prostokątnych?
Powtórzmy eksperyment z obracaniem płaskiego obiektu, obserwujmy jak rzutowane są jego krawędzie, czyli linie i wyciągajmy wnioski:
a) przedstawiono na nim odcinek linii prostej równoległy do płaszczyzny projekcji w naturalnych rozmiarach (porównaj wysokość obiektu AD i BC na ryc. 109, a, b, c z jego rzutami a'd' i b'c, oraz szerokość obiektu AB i CD z jego występami a'b' i c'd' na ryc. 109, a);
b) przedstawiono na nim prosty odcinek nachylony do płaszczyzny projekcji ze zniekształceniem długości (porównaj szerokość obiektu AB i CD na ryc. 109, b z jego rzutami a’b’ i c’d’);
c) odcinek linii prostej prostopadły do płaszczyzny projekcji jest przedstawiony na nim przez punkt (patrz ryc. 109 na szerokości obiektu - linie AB i CD, prostopadłe do płaszczyzny projekcji).
Rzut punktu to podstawa prostopadłej obniżonej z danego punktu w przestrzeni na płaszczyznę rzutu (patrz punkty a’, b’, c’, d’ – rzuty punktów A, B, C, D).
Zgódźmy się oznaczać punkty w przestrzeni wielkimi literami A, B, C, D itd., a rzuty punktów odpowiednimi małymi literami i, b, c, d itd.
Z dwóch punktów pokrywających się na rysunku (ryc. 109, c), jeden jest obrazem widocznego wierzchołka, a drugi jest niewidoczny (zamknięty). Oznaczenie rzutów niewidocznych wierzchołków podano w nawiasach.



