Secties: Technologie
Doelen en doelstellingen van de les:
leerzaam: laat leerlingen zien hoe ze de rechthoekige projectiemethode kunnen gebruiken bij het maken van een tekening;
• de noodzaak om drie projectievlakken te gebruiken;
• voorwaarden creëren voor de vorming van vaardigheden om een object op drie projectievlakken te projecteren;
ontwikkelen: ruimtelijke concepten, ruimtelijk denken, cognitieve interesse en creatieve vaardigheden van studenten ontwikkelen;
opleiden: verantwoordelijke houding ten opzichte van tekenen, om een cultuur van grafisch werk te cultiveren.
Lesmethoden en -technieken: uitleg, conversatie, probleemsituaties, onderzoek, oefeningen, frontaal werk met de klas, creatief werk.
Materiële ondersteuning: computers, presentatie “Rechthoekige projectie”, taken, oefeningen, oefenkaarten, presentatie voor zelftest.
Lestype: les om kennis te consolideren.
Woordenschatwerk: horizontaal vlak, projectie, projectie, profiel, onderzoek, project.
I. Organisatorisch gedeelte.
Geef het onderwerp en het doel van de les aan.
Laten we uitvoeren les-competitie, voor elke taak ontvang je een bepaald aantal punten. Afhankelijk van de behaalde punten wordt er een cijfer voor de les toegekend.
II. Herhaling van projectie en zijn typen.
Projectie is het mentale proces waarbij afbeeldingen van objecten in een vlak worden geconstrueerd.
Herhaling wordt uitgevoerd met behulp van presentatie.
1. Er wordt aan studenten gevraagd problematische situatie. (Presentatie 1)
Analyseer de geometrische vorm van het onderdeel op de frontprojectie en vind dit onderdeel tussen de visuele afbeeldingen.

Uit deze situatie wordt geconcludeerd dat alle 6 delen dezelfde frontale projectie hebben. Dit betekent dat één projectie niet altijd een volledig beeld geeft van de vorm en het ontwerp van het onderdeel.
- Wat is de uitweg uit deze situatie? (Kijk naar het onderdeel vanaf de andere kant).
2. Er was behoefte aan een ander projectievlak. (Horizontale projectie).
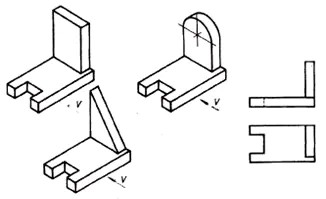
3. De behoefte aan een derde projectie ontstaat wanneer twee projecties niet voldoende zijn om de vorm van een object te bepalen.
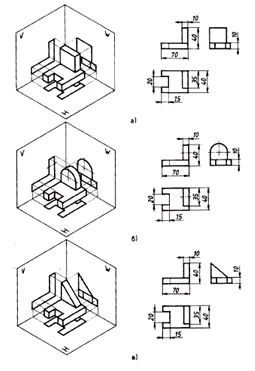
Maatvoering:
- op de frontale projectie –
Conclusie: dit betekent dat je, om te leren tekenen, objecten op een vlak moet kunnen projecteren.
Vul de ontbrekende woorden in de definitietekst in.
1. Er zijn _______________ en _____________ projectie.
2. Als er ______________ stralen uit één punt komen, wordt projectie ______________ genoemd.
3. Als ______________ stralen parallel worden gericht, wordt projectie _____________ genoemd.
4. Als ______________ stralen evenwijdig aan elkaar en onder een hoek van 90 ° ten opzichte van het projectievlak worden gericht, wordt de projectie ______________ genoemd.
5. Een natuurlijk beeld van een object op een projectievlak wordt alleen verkregen met _____________ projectie.
6. De uitsteeksels bevinden zich ten opzichte van elkaar______________________________.
7. De grondlegger van de rechthoekige projectiemethode is _______________
Taak 2. Onderzoeksproject
Zorg ervoor dat de hoofdtypen, aangegeven met cijfers, overeenkomen met de onderdelen die met letters worden aangegeven, en schrijf het antwoord in je notitieboekje.
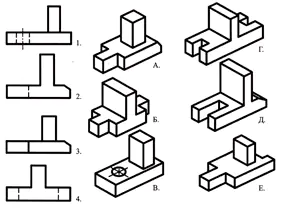
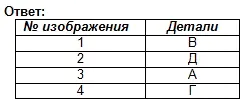
Een oefening om de kennis van geometrische lichamen te herzien.
Zoek met behulp van de verbale beschrijving een visueel beeld van het onderdeel.
De basis van het onderdeel heeft de vorm van een rechthoekig parallellepipedum, waarvan de kleinere vlakken groeven hebben in de vorm van een regelmatig vierhoekig prisma. In het midden van het bovenvlak van het parallellepipedum bevindt zich een afgeknotte kegel, langs de as waarvan zich een doorgaand cilindrisch gat bevindt.
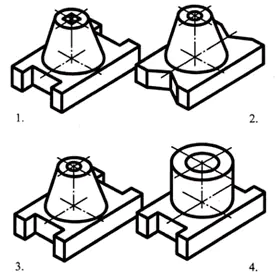
Antwoord: deel nr. 3 (1 punt)
Zoek de overeenkomst tussen de technische tekeningen van de onderdelen en hun frontale projecties (de projectierichting is gemarkeerd met een pijl). Maak op basis van de verspreide afbeeldingen van de tekening een tekening van elk onderdeel, bestaande uit drie afbeeldingen. Schrijf uw antwoord in de tabel (Afb. 129).
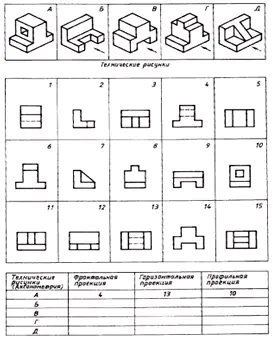
| Technische tekeningen | Frontale projectie | Horizontale projectie | Profielprojectie |
| A | 4 | 13 | 10 |
| B | 12 | 9 | 2 |
| IN | 14 | 5 | 1 |
| G | 6 | 15 | 8 |
| D | 11 | 3 | 7 |
III. Praktisch werk.
Taak nr. 1. Onderzoeksproject
Zoek de frontale en horizontale projecties voor dit visuele beeld. Schrijf het antwoord in je notitieboekje.
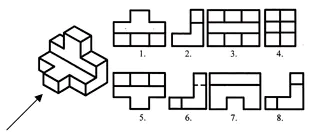
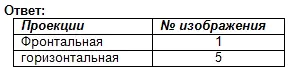
Beoordeling van het werk in de les. Zelftest. (Presentatie 2)
De punten voor het beoordelen van het eerste deel van het werk staan op het bord:
Taak nr. 2. Creatief werk en verificatie van de implementatie ervan
(creatief project)
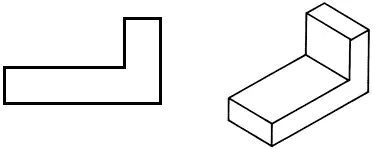
• Teken de frontale projectie in je werkboek.
• Teken een horizontale projectie, waarbij u de vorm van het onderdeel verandert om de massa ervan te verminderen.
• Breng indien nodig wijzigingen aan in de frontale projectie.
• Om de voltooiing van de taak te controleren, roept u een of twee leerlingen naar het bord om hun oplossing voor het probleem uit te leggen.
IV. De les samenvattend.
1. Beoordeling van werk in de les. (Het praktische deel van het werk controleren)
V. Huiswerkopdracht.
1. Onderzoeksproject.
Werk volgens de tabel: bepaal welke tekening, aangegeven met een cijfer, overeenkomt met de tekening, aangegeven met een letter.
Er wordt een speciaal geval van parallelle projectie genoemd, waarbij de projectierichting loodrecht op het projectievlak staat rechthoekig of orthogonale projectie. De rechthoekige (orthogonale) projectie van een punt is de basis van de loodlijn die van het punt naar het projectievlak wordt getrokken. De rechthoekige projectie van de punten A en B wordt getoond in Fig. 5.
Om de positie van een punt in de ruimte te bepalen op basis van zijn parallelle projecties, is het noodzakelijk om twee evenwijdige vlakken te verkrijgen in twee projectierichtingen.
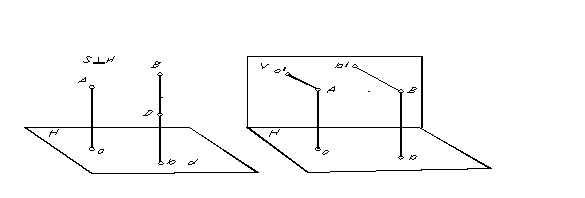 |
Omdat door een punt kan slechts één rechte lijn loodrecht op het vlak worden getekend. Vervolgens is het uiteraard met orthogonale projectie noodzakelijk om twee niet-parallelle projectievlakken te hebben om twee projecties van één punt te verkrijgen (Fig. 6) .
Orthografische projectie heeft een aantal voordelen ten opzichte van centrale en parallelle projectie. Deze omvatten voornamelijk:
1. Eenvoud van grafische constructies voor het bepalen van orthogonale projecties van punten.
2. Het vermogen, onder bepaalde omstandigheden, om de vorm en grootte van de geprojecteerde figuur op projecties te behouden.
De genoemde voordelen hebben gezorgd voor een wijdverbreid gebruik van orthogonale projectie in de technologie, in het bijzonder voor het maken van werktuigbouwkundige tekeningen.
Om in de machinebouw de vorm en grootte van de afgebeelde objecten aan de hand van een tekening te kunnen beoordelen, gebruiken ze bij het maken van tekeningen in de regel niet twee, maar meerdere projectievlakken.
De positie van een punt in de ruimte, en dus van elke geometrische figuur, kan worden bepaald als er een coördinatenreferentiesysteem wordt gespecificeerd. Projectievlakken verdelen de ruimte in acht delen: octanten. Ze zijn conventioneel genummerd met Romeinse cijfers (Fig. 7).
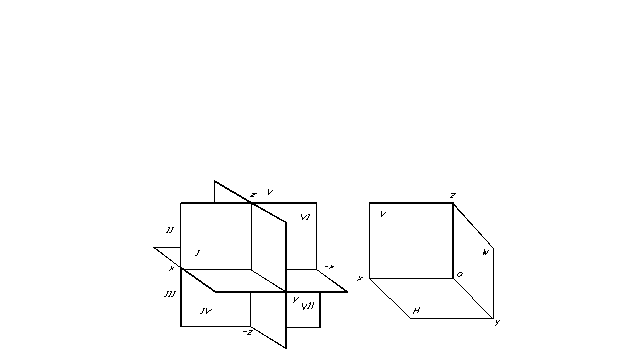
Projectievlakken verdelen de ruimte in acht delen: octanten. Ze zijn conventioneel genummerd met Romeinse cijfers (Fig. 7).
Het handigste voor het vaststellen van de positie van een geometrische figuur in de ruimte en het identificeren van de vorm ervan op basis van orthogonale projecties is het Cartesiaanse coördinatensysteem, dat bestaat uit drie onderling loodrechte projectievlakken. Vanwege het feit dat de beschrijvende meetkunde is ontworpen om de resultaten van haar theoretisch onderzoek voor praktisch gebruik over te brengen, is het raadzaam om orthogonale projectie ook in een systeem van drie projectievlakken te overwegen.
Voor het gemak van projectie zijn drie onderling loodrechte vlakken gekozen als drie projectievlakken (Fig. 8). Een ervan wordt meestal horizontaal geplaatst - het wordt genoemd horizontaal projectievlak, de andere is verticaal, evenwijdig aan het tekenvlak, heet dat frontaal vlak van projecties en een derde, loodrecht op de twee bestaande, heet profielvlak van projecties. Deze projectievlakken snijden elkaar langs zogenaamde lijnen projectie assen.
We hebben een rechtshandig systeem toegepast voor het rangschikken van projectievlakken. In dit geval wordt rekening gehouden met de positieve richtingen van de assen: voor de as X (snijpunt van horizontale en frontale projectievlakken) – links van de oorsprong, voor de as j (snijpunt van horizontale en profielprojectievlakken) – richting de waarnemer vanuit het frontale projectievlak, voor de as z (snijpunt van de frontale en profielvlakken van projecties) – omhoog vanuit het horizontale vlak van projecties worden de tegenovergestelde richtingen van de assen als negatief beschouwd.
De projectie van een punt is de basis van de loodlijn die vanaf het punt op het overeenkomstige projectievlak wordt getrokken. Horizontale projectie punten zijn de rechthoekige projectie van een punt op een horizontaal projectievlak, frontale projectie – respectievelijk op het frontale vlak van projecties en profiel – op het profielvlak van projecties.
Het is lastig om deze ruimtelijke lay-out te gebruiken om orthogonale projecties van geometrische figuren weer te geven vanwege de omvang ervan, en ook vanwege het feit dat op individuele (horizontaal en profiel) de vorm en grootte van de geprojecteerde figuur vervormd zijn. Daarom gebruiken ze, in plaats van een ruimtelijke indeling in een tekening weer te geven, een complexe tekening (Monge-diagram) die bestaat uit drie onderling verbonden orthogonale projecties van een geometrische figuur.
De transformatie van de ruimtelijke indeling in diagrammen wordt uitgevoerd door de horizontale en profielprojectievlakken te combineren met het frontale projectievlak (Fig. 7).
Omdat de vlakken geen grenzen hebben, worden in de gecombineerde positie (op het diagram) de grenzen van de vlakken niet weergegeven, het is niet nodig om inscripties achter te laten die de positie van de projectievlakken aangeven (Fig. 10).
Nadat ik naar het diagram was overgestapt, ging de ruimtelijke helderheid verloren. Het diagram geeft meer: nauwkeurigheid en gemak van het meten van afbeeldingen, met eenvoud van constructie. Om een ruimtelijk beeld voor te stellen is echter verbeeldingskracht nodig.
Niet gevonden wat u zocht? Gebruik de zoekopdracht:
Beste uitspraken: Voor een student is het belangrijkste niet om het examen te halen, maar om er op tijd aan te denken. 9744 — | 7364 - of lees alles.
Projectietekening (basisprincipes van beschrijvende geometrie)
Projectie methode
Rechthoekige projectiemethode
Als de projecterende stralen een rechte hoek maken met het projectievlak, worden dergelijke projecties genoemd rechthoekig.
Rechthoekige projecties worden ook wel genoemd orthogonaal. Het woord "orthogonaal" komt van de Griekse woorden "ortos" - recht en "gonia" - hoek.
Tekeningen in het systeem van rechthoekige projecties geven een compleet beeld van de vorm en grootte van het object. Ze zijn gemakkelijker uit te voeren dan axonometrische projecties.
Wat moet je weten om tekeningen succesvol af te ronden?
Elk object met vlakke oppervlakken wordt beperkt door hoekpunten, randen en vlakken (Fig. 108). Om te leren hoe je verschillende objecten in tekeningen kunt weergeven, moet je daarom weten hoe hoekpunten (punten), randen (segmenten van rechte lijnen) en randen van objecten (delen van een vlak) worden weergegeven in rechthoekige projecties.
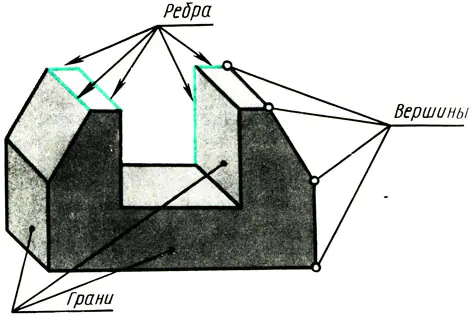
Rijst. 108. Premsch als een reeks punten, schrijf. Hoekpunten van vlakken
Laten we een eenvoudig experiment doen. Laten we eens kijken hoe een plat object en honderd elementen in verschillende posities worden weergegeven.
Laten we de muur tegenover het raam als projectievlak nemen. Laat het uit het raam komen loodrecht Lichtstralen vallen op de muur en projecteren stralen. Plaats een vel dik ABCD-papier voor de muur (parallel daaraan) (afb. 109, a). Er ontstaat een schaduw op de muur, gelijk aan de projectie van het object. Wat zijn de afmetingen? In dit geval komt de projectie a’b’c’d’ qua vorm en grootte overeen met het projectieobject: het vel
ABCD. De projectiemethode is rechthoekig, omdat de projecterende stralen loodrecht op het projectievlak staan.
Hoe zal de projectie veranderen als het afgebeelde object bijvoorbeeld rond zijn hoogte wordt geroteerd - rand AD (Fig. 109, b)?
Bij het draaien zal de schaduw in de breedte krimpen (de lijnen a’b’ en c’d’ in Fig. 109, b worden korter). Als we het vel papier blijven roteren, merken we op dat in een positie loodrecht op de muur het beeld van het vel in een lijn zal veranderen (Fig. 109, c), maar de hoogte van het object blijft constant, d.w.z. lijnen a' d' en b'c' over de lengte zijn niet vervormd.
Laten we nu conclusies formuleren over welke vorm en grootte afbeeldingen een plat object heeft in rechthoekige projecties, verschillend geplaatst ten opzichte van het projectievlak:
a) daarop wordt een platte figuur evenwijdig aan het projectievlak in natuurlijke grootte afgebeeld (Fig. 109, a);
b) daarop wordt een platte figuur afgebeeld, hellend ten opzichte van het projectievlak, met een vervorming van de afmetingen (Fig. 109, b);
c) daarop wordt een platte figuur loodrecht op het projectievlak afgebeeld in de vorm van een recht lijnsegment (Fig. 109, c).
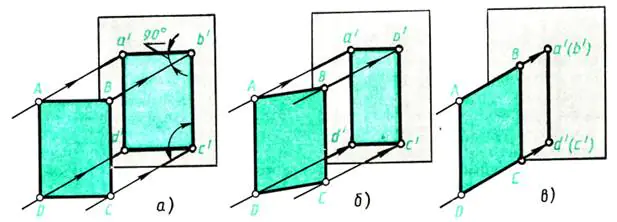
Rijst. 109. Een plat figuur projecteren
Deze bevindingen hebben betrekking op de weergave van de randen van objecten.
Hoe worden de randen van objecten, dat wil zeggen lijnen, weergegeven in rechthoekige projecties?
Laten we het experiment herhalen met het roteren van een plat voorwerp, observeren hoe de randen, dat wil zeggen lijnen, worden geprojecteerd en conclusies trekken:
a) daarop is een recht lijnsegment evenwijdig aan het projectievlak afgebeeld in natuurlijke grootte (vergelijk de hoogte van het object AD en BC in figuur 109, a, b, c met zijn projecties a'd' en b'c, en de breedte van het object AB en CD met zijn uitsteeksels a'b' en c'd' in figuur 109, a);
b) daarop wordt een recht segment afgebeeld dat schuin staat ten opzichte van het projectievlak met een lengtevervorming (vergelijk de breedte van het object AB en CD in figuur 109, b met zijn projecties a'b' en c'd');
c) een recht lijnsegment loodrecht op het projectievlak wordt weergegeven door een punt erop (zie in figuur 109, over de breedte van het object - lijnen AB en CD, loodrecht op het projectievlak).
De projectie van een punt is de basis van een loodlijn die vanaf een bepaald punt in de ruimte op het projectievlak wordt neergelaten (zie punten a’, b’, c’, d’ - projecties van punten A, B, C, D).
Laten we ermee instemmen punten in de ruimte aan te duiden met hoofdletters A, B, C, D, enz., en projecties van punten met de overeenkomstige kleine letters i, b, c, d, enz.
Van de twee punten die samenvallen in de tekening (Fig. 109, c), is er één een afbeelding van een zichtbaar hoekpunt, en de andere is een onzichtbaar (gesloten) punt. De aanduiding van projecties van onzichtbare hoekpunten staat tussen haakjes.



